03.B树

翻译自《build your own database from scratch》, 转代码为C++

03. B-Tree: The Ideas

3.1 B树和BST树

　　首先介绍的知识是平衡二叉树（BST）。二叉树是用于排序数据的常用数据结构。插入或移除键后保持树的良好形状就是“平衡”的含义。如前一章所述，为了利用“页面”（IO的最小单位），应该使用n元树而不是二叉树。B树可以从BST中推广。B树的每个节点都包含多个key和多个指向其子节点的链接。在节点中查找关键字时，所有关键字都用于决定下一个子节点。

　　​​

　　B树和BST的平衡不同，像RB树或AVL树这样的流行BST是在子树的高度上平衡的（通过旋转）。虽然所有B树叶节点的高度都是相同的，但B树是由节点的大小来平衡的：

• 如果一个节点太大，无法放在一个页面上，则将其拆分为两个节点。如果根节点被拆分，这将增加父节点的大小，并可能增加树的高度。
• 如果节点太小，请尝试将其与同级节点合并。

　　如果您熟悉RB树，您可能也知道2-3树可以很容易变成B树。

3.2 B树和嵌套数组

　　即使你不熟悉2-3树，你仍然可以使用嵌套数组获得一些了解。让我们从一个排序数组开始。查询可以通过平分来完成。但是，更新数组是我们需要处理的O（n）。更新一个大数组是不好的，所以我们把它分成更小的数组。假设我们将数组拆分为sqrt（n）个部分，每个部分平均包含sqrt（n）个键

　　[[1,2,3]，[4,6]，[9,11,12]]

　　要查询key，我们必须首先确定哪个部分包含key，在sqrt（n）部分上平分为O（log（n））。在那之后，将零件上的键一分为二再次为O（log（n））——这并不比以前更糟。并且更新被改进为O（sqrt（n））。这是一个2级排序的嵌套数组，如果我们添加更多的级别呢？这是B树的另一种直观的解释。

3.3 B树操作

　　查询B树与查询BST是相同的。

　　但是更新B-树要更复杂。从现在起，我们将使用一种称为“B+树”的B树变体，B+树只在叶节点中存储值，而内部节点只包含key。

　　从叶子节点开始插入key。叶子只是key的排序。把key插进叶子节点里是件小事，但是，插入可能会导致节点大小超过页面大小。在这种情况下，我们需要将叶节点拆分为2个节点，每个节点包含一半的key，这样两个叶节点就可以放在一个页面中。

　　内部节点包括：

　　1、子节点的指针列表。

　　2、与指针列表配对的key列表。每个key都是相应子项的第一个key

　　在将叶节点分割为两个节点之后，父节点用新的指针和key替换旧的指针和key。节点的大小增加，这可能触发进一步的分割。

　　​​

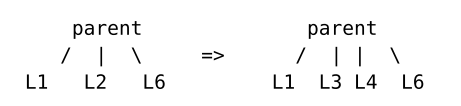
　　拆分根节点后，将添加一个新的根节点。B树就是这样生长的。

　　​​

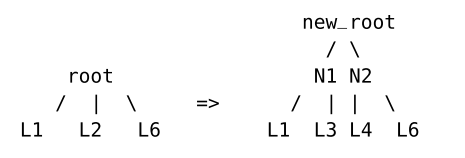
　　删除key与插入相反。节点从不为空，因为小节点将合并到其左同级或右同级中。当一个非叶根被简化为一个key时，这个根可以被它唯一的子代代替。这就是B树收缩的方式。

3.4 不可变数据结构

　　不可变意味着永远不会适时地更新数据。一些类似的术语是“append-only”、“copy-on-write”和“persistent data structures”(“持久”这个词与我们之前讨论的“持久”没有任何关系)。

　　例如，将键插入叶节点时，不要原地修改节点，而是使用要更新的节点中的所有key和新key创建一个新节点。现在，父节点也必须更新以指向新节点。同样，父节点也会使用新指针进行复制。在我们到达根节点之前，整个路径都是重复的。这有效地创建了一个与旧版本共存的新版本的树。

　　可变数据结构有几个优点：

1、避免数据损坏。不可变数据结构不会修改现有数据，它们只是添加新数据，因此即使更新中断，旧版本的数据也保持不变。  
2、易于并发。读者可以与写者同时操作，因为读者可以不受影响地处理旧版本。  

持久性和并发性将在后面的章节中介绍。现在，我们将首先编写一个不可变的B+树。

　　‍