光线追踪(三) 微平面理论

基于物理的渲染：微平面理论（Cook-Torrance BRDF推导)

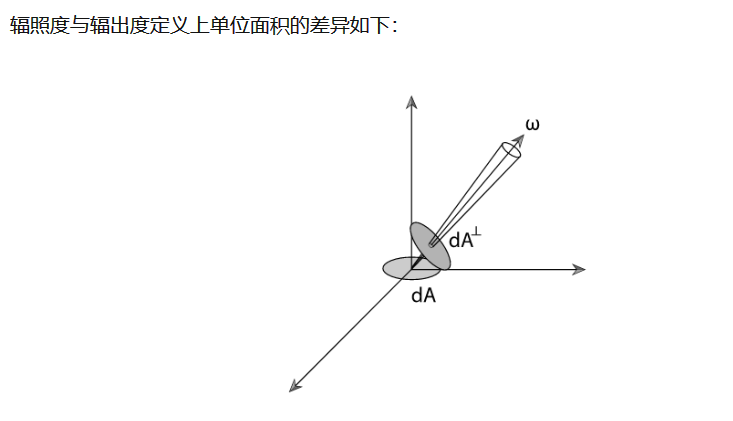
辐射度量基础概念总结

微平面理论

微平面理论(Microfacets Theory)顾名思义，就是从微观的角度去分析，其认为任意物体的表面在到达微观的尺度之后，都是由许许多多的更小的镜面所组成的

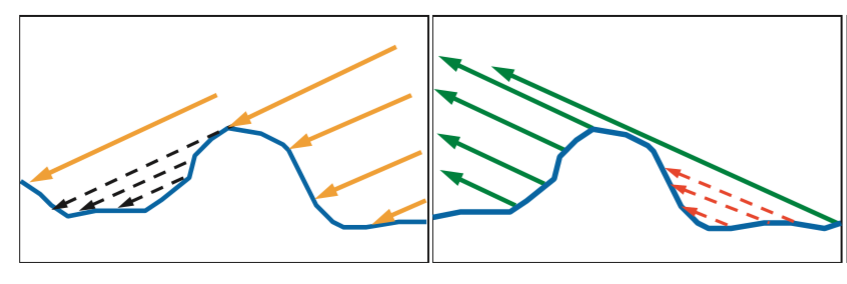
当这些微小的镜面的法线方向较为集中一致的时候，从宏观角度来看，物体的镜面反射会比较明显，反之，当这些微小镜面的法线方向较为杂乱，分布均匀的时候，物体表面则会相对粗糙。如下图所示：

（上方图中，微平面的镜面法线方向比较集中，下方图中微平面的镜面法线方向比较分散）

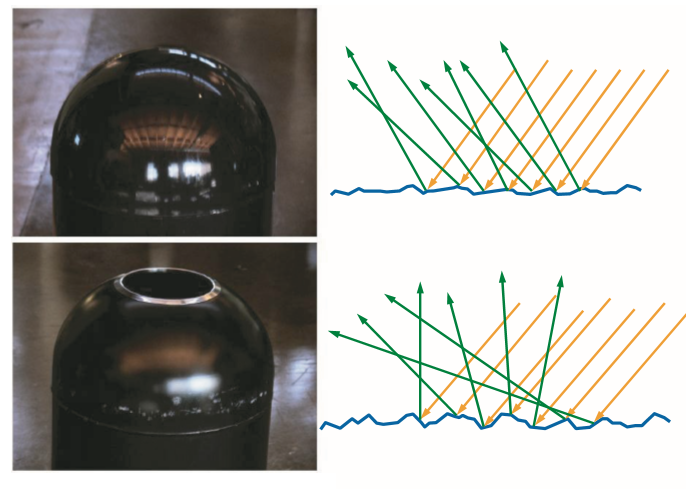
对于微观尺度的漫反射可以作如下解释，当光线照射到物体表面时，一部分光线会与表面的许许多多的微小镜面发生镜面反射，另一部分光线则会折射进入物体内部，如下图：

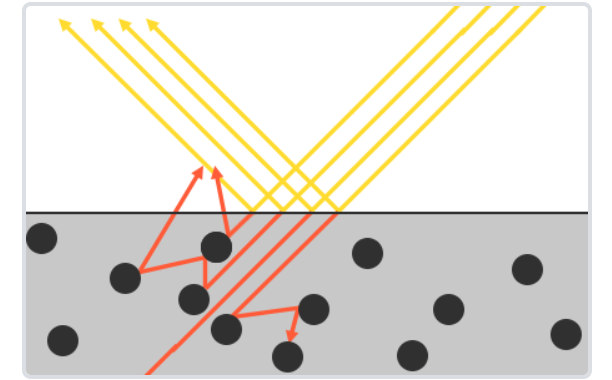
当光线折射进入内部的时候会与物体的微小粒子不断发生碰撞并散射到随机方向，同时在碰撞的过程中一部分光线的能量会被吸收转换为热能，有些光线在多次碰撞之后能量消耗殆尽，则表示该光线完全被物体吸收。还有一部分折射到物体内部的光线会因为散射方向的随机性重新离开表面，而这部分光线就形成了漫反射。 (tips:光线折射进入物体内部之后再被散射出来，离开表面的点可能并不是进入表面的点，但这里并不考虑这种情形，次表面散射(Subsurface Scattering)技术则将这种现象考虑了进去。)

Cook-Torrance BRDF推导

漫反射项推导

漫反射会均匀的向每个方向反射，因此，漫反射的BRDF一定是一个常数。假设入射光是均匀且遍布整个半球方向，可以得到如下方程：

镜面反射项推导

函数D：法线分布函数(Normal Distribution Function)，其代表了所有微观角度下微小镜面法线的分布情况，粗糙表面法线分布相对均匀，光滑表面法线分布相对集中 (这种解释可能会有些抽象，后面会给出更加直观的物理上的解释)

函数G：几何函数(Geometry Function)，描述了微平面自遮挡的属性。当一个平面相对比较粗糙的时候，平面表面上的微平面有可能挡住其他的微平面从而减少表面所反射的光线。

函数F：菲涅尔方程(Fresnel Rquation)，描述了物体表面在不同入射光角度下反射光线所占的比率

可以看出无论是几何函数G，还是菲涅尔方程F，都是由于观察方向，入射方向的不同所导致的只有部分光线能够被反射

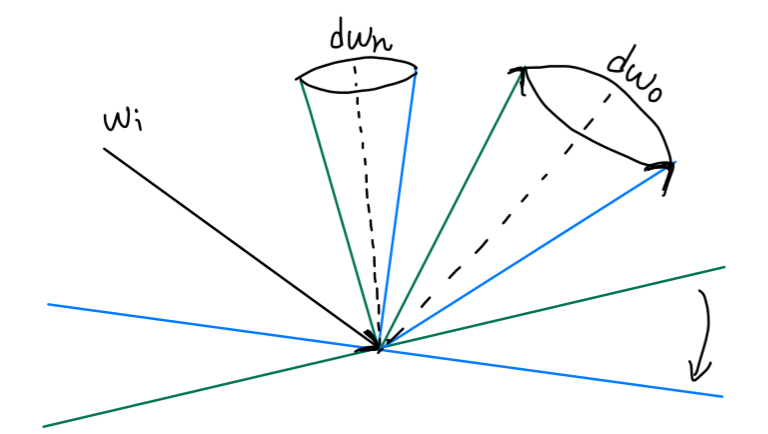
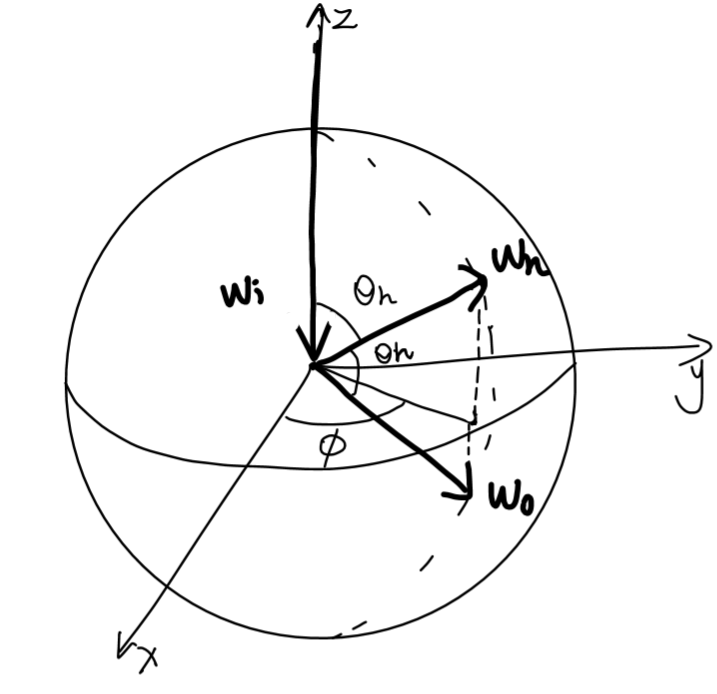
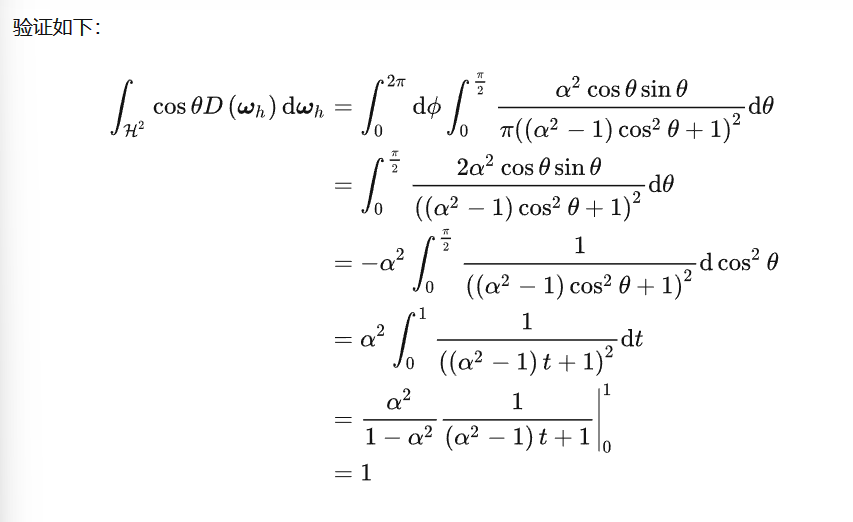
菲涅尔方程与几何函数的补充

菲涅尔方程

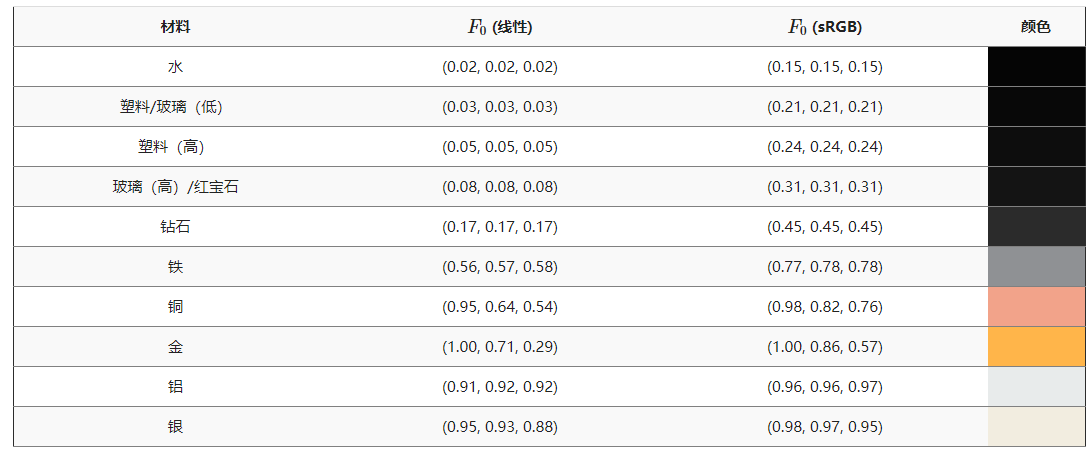
几何函数

几何函数G是为了表示微平面的自遮挡从而引起的光线损失，一般会出现如下两种的遮挡情况