光线追踪(一) Whitted-style Ray Tracing
Whitted-style Ray Tracing
主要参考链接:
计算机图形学十二:Whitted-Style光线追踪原理详解及实现细节
计算机图形学GAMES101(十四)光线追踪(辐射度量学、渲染方程与全局光照)_辐射度量学与图形学_momohola的博客-CSDN博客
计算机图形学GAMES101(十五)光线追踪(蒙特卡洛积分与路径追踪)_momohola的博客-CSDN博客
作业解析:
Games 101 | 作业5 + 光线追踪 Ray Tracing
Whitted-Style Ray Tracing
为什么?
光栅化很难处理全局光照(也有一些奇技淫巧,但是不能保证正确性)
Soft Shadows
Glossy reflection
Indirect Illumination
光栅化:快速近似、质量低
光线追踪:准确、非常慢
offline渲染
实际生产中,渲染电影的一帧=~10000CPU小时
原理
首先对光线进行一些假设:
光线一定沿着直线传播
光线之间无法碰撞
光线路径可逆,即从A发出的到B的光线,一定也可以从B发出到A(中途可发生反射和折射)
考虑一下对光线的第三条假设:光路可逆,所有进入到人眼的光,都可从人眼发出光按照原路反方向返回,那么利用这种模拟从人眼发射光线的方法不就可以还原出所有的光路了呢?没错这就是光线追踪的核心想法,从光源出发难以模拟那就反着从摄像机发射光线!
Ray Casting
从人眼或摄像机向近投影平面上的每一个像素点发射一条光线,判断与场景物体的交点。当然一条光线自然可能会与不止一个物体相交,但是考虑遮挡关系,只去找最近的交点。接着连接该交点和光源,只要判断这条连线之间是否有物体存在就可以知道该交点是否在阴影之中。
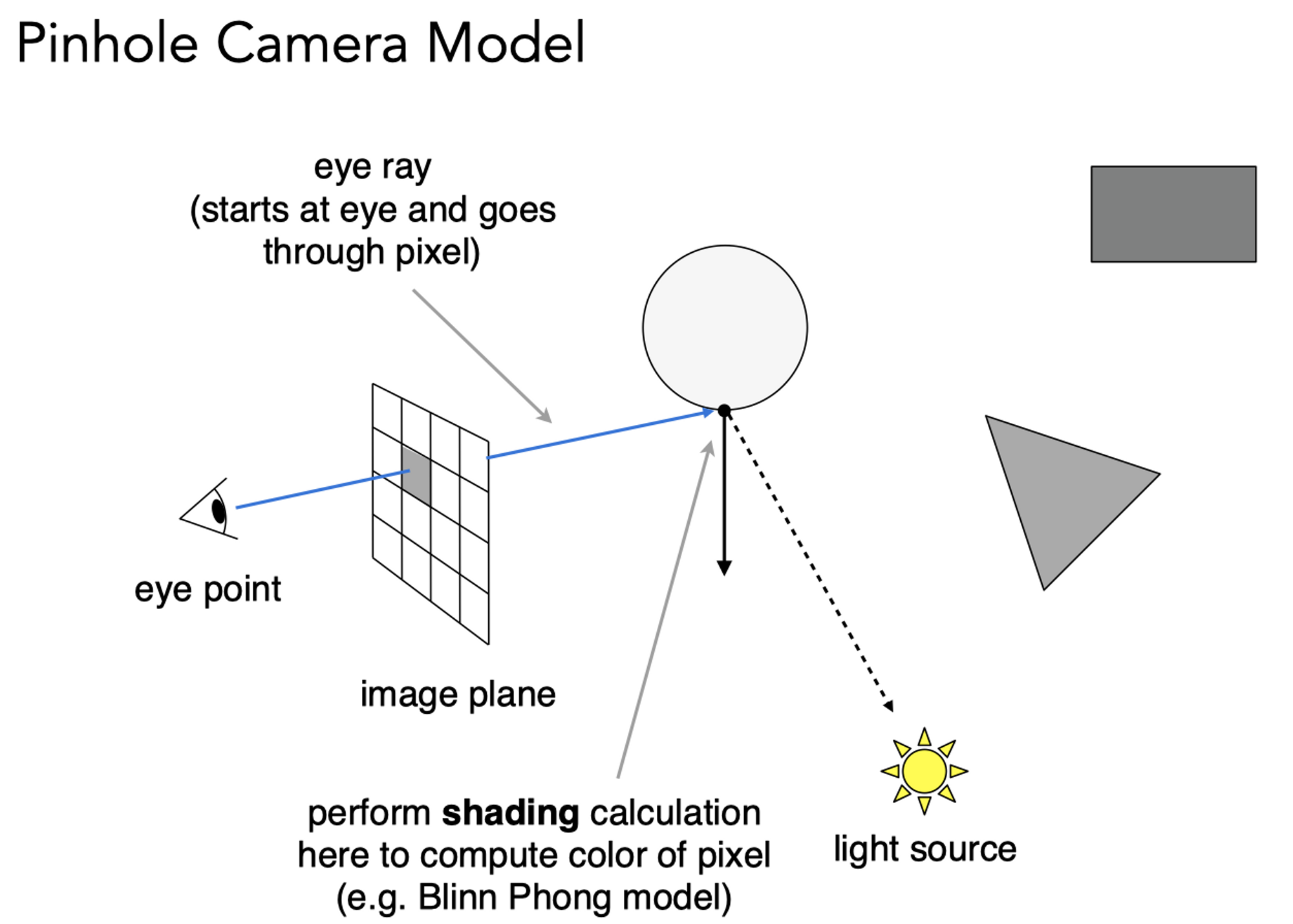
紧接着,自然可以利用Blinn-Phong模型对这个点进行局部光照模型计算,得到该像素的颜色,那么遍历所有近投影平面上的像素就能得到一张完整的图像。但如果光线追踪仅仅是在第一步Ray Casting就停止的话,那么它的效果与局部光照模型是一样的,因此我们需要第二步,真正的考虑全局效果
Recursive (Whitted-Style) Ray Tracing
考虑第一步中所做的Ray Casting,该条光线第一个与圆球物体相交,假设该圆球是一个玻璃球,那么便会发生镜面反射和折射。反射与折射出去的光线会可能与场景中的物体再次碰撞,发生第二次折射与反射。
光线弹射多次:Recursive (Whitted-Style) Ray Tracing
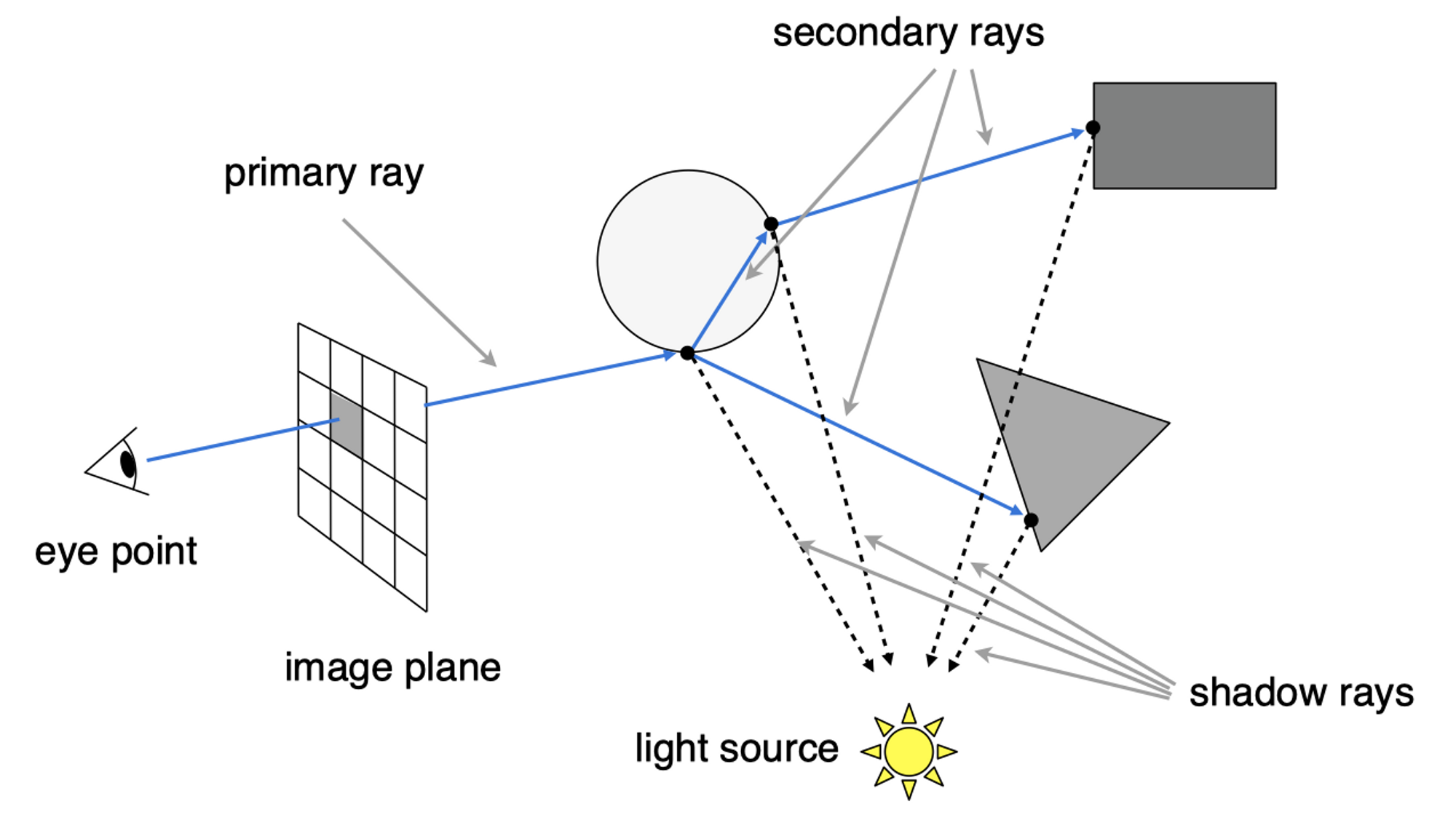
从图中可以见到,不仅仅是与圆球相交的那一点可以贡献光到达眼睛,折射与反射之后再与物体相交的点也可以贡献光(光路可逆原理)。简而言之,除了直接从光源照射到圆球交点再沿着 eye rays(从眼睛发射的第一条光线)到眼睛中,也可能存在这样一种情形,有光照射到其他物体,再沿着eye rays的反射或折射的光线方向传回人眼!
因此每一个交点的颜色贡献来自这样种几类型 直接光照,反射方向间接光,折射方向间接光(如果有折射的话)
下一步将这些所有交点与光源连接,称这些线为shadow rays(因为可以用来检测阴影),计算这些所有点的局部光照模型的结果,将其按照光线能量权重累加(该做法与递归过程等价),最终得到近投影平面上该像素点的颜色!而这就是一个考虑全局效果的光照模型了,因为不仅仅考虑了直接光源的贡献,还考虑各种折射与反射光线的贡献。
以上就是光线追踪的整个过程了,还有额外几点要注意的 tips:
整体过程是一个递归的过程,因此需要一定的递归终止条件,比如说允许的最大反射或折射次数为10。
光线在每次反射和折射之后都有能量损耗的,由系数决定,因此越往后的折射和反射光贡献的能量越小,这也是为什么在上文中提到根据光线能量权重求和。 e.g. 反射系数为0.7,那么第一次反射折损30%,第二次反射折损1-(70%x70%),依次类推。
如果反射或折射光线没有碰撞到物体,一般直接返回一个背景色
参考伪代码如下:

光线的表示方法
我们可以将每一条光线想象成一条射线,那么每一条光线都会由起点及方向这两个属性所固定,如下图所示:
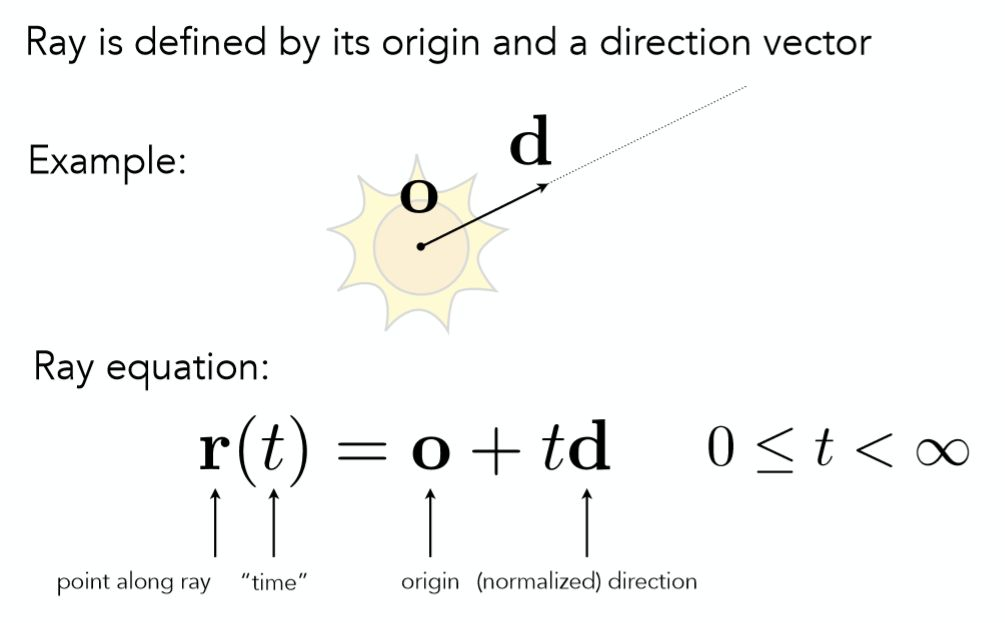
起点o,方向d
光线如何与物体求交
隐式表面求交
首先介绍如何计算光线与隐式曲面的交点的方法,以一个球体为例,二者表示方程如下:
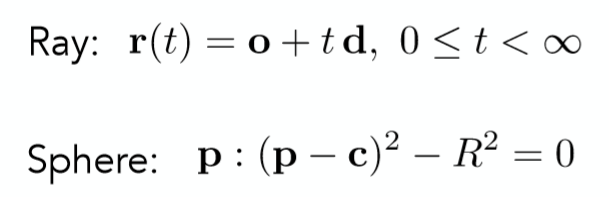
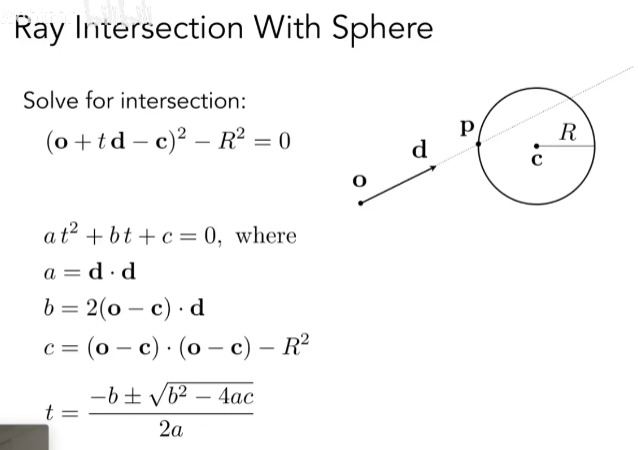
同样的根据b2-4ac 的正负关系,即可判断光线与球是一个交点还是两个交点又或是没有交点
进一步推广到隐式表面

显式表面求交
真正在图形学中大量运用的其实是显示曲面,更具体来说就是许许多多个三角形,因此如何判断一条光线与显示曲面的交点,其实也就是计算光线与三角形面的交点。对于任意一个平面,可以用如下图中的式子表达:

图中对于平面方程的讲解已经很清楚。那么到这里其实已经成功把对显示曲面的求交又转化为了类似隐式曲面求交的方法,对于任意一个三角面来说,它一定处于一个平面之上,只需求出光线与平面的交点,再判断该交点是否在三角形内,就可以得到光线是否与三角形面相交的结果了!
首先给出如何计算光线与平面交点的过程:
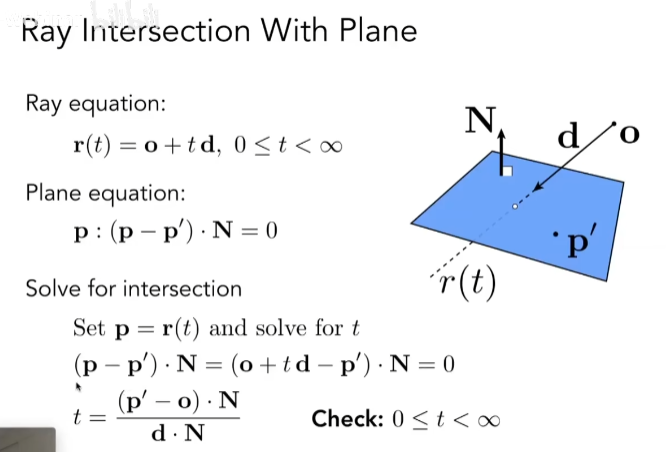
得到参数 t 之后,自然可以计算出交点,并且再去计算出重心坐标就能判断该交点是否在三角形内了,但是这种方法略显繁琐,能不能一步就得到结果呢?当然可以!

直接将点的形式用重心坐标的形式表示,随后利用克莱姆法则求解线性方程组即可!
判断合理:t为正
判断在三角形内:重心坐标三个系数均为正
推导过程:
反射和折射
反射方向计算
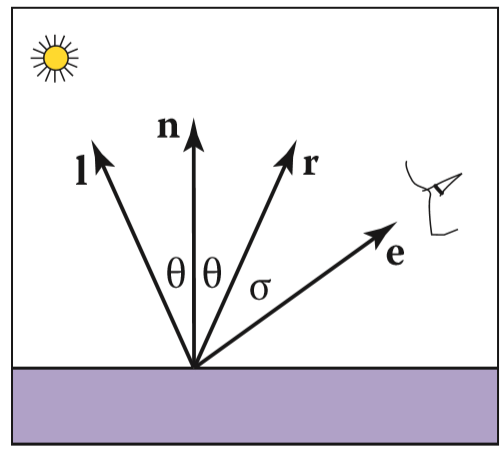

折射方向计算
折射方向的推导其实是由斯奈尔定理(Snell’s Law)得来的:
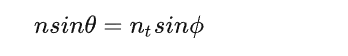
n,nt分别表示反射平面两边的反射率。
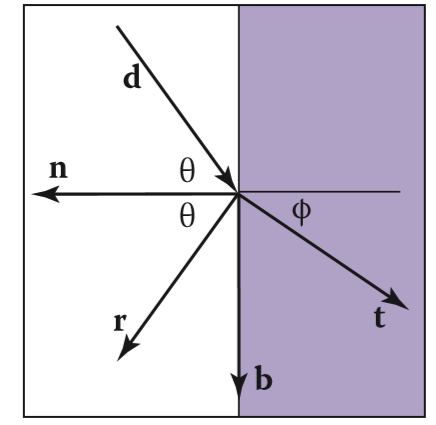

菲涅尔反射

如果你垂直观察玻璃,你很容易看清玻璃外的东西(折射而来),如果你视线玻璃近乎平行,此时你看到的大部分会是你自己(反射得到),且视线越与玻璃平行,即与法线夹角越大,你的人像越加清晰,这种现象,就可以用菲涅尔反射来进行解释
简单来说,便是物体的反射率其实与你的观察角度即有关,对于绝缘体来说观察角度与法线夹角越大,反射的程度就越大
金属反射率一直很大,所以很有光泽。
那么对于任意一个物体该去怎么计算出它的精确的反射率呢?计算公式如下:

当然这里考虑了两个极化,然后再求平均,我们不需要知道为什么要这么算,只要知道,物体的反射率和入射角度,和入射空间的折射率,和物体的折射率有关就可以了,然后套公式算就能得出正确的反射率了!那么对于精确的算法来说,可以看到计算量是非常大的,因此就有大佬提出了个简单的算法,近似得到结果,但计算量大大减小,如下:
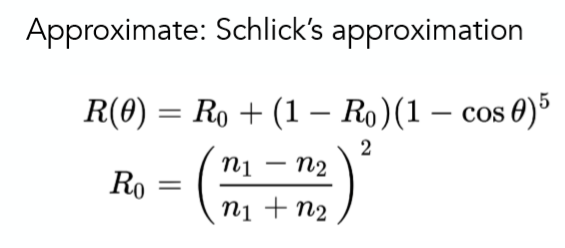
如何考虑漫反射
在Blin-Phong模型中层提到过,漫反射是光线照射到粗糙物体表面从而发生向周围均匀反射光线的一种现象,反射的光线可以说是无数的!
那么对于这种反射,在光线追踪该怎么处理呢?借鉴RayTracingInOneWeekend 里的做法,对于漫反射表面每次进行反射的时候,随机的选取物体表面向外半圆内的一个方向作为该次反射的方向,对其再像镜面反射及折射一样进行递归的光线追踪计算。
但对每一个像素不仅仅只发出一条感知光线,利用多条光线RayTracing的结果求均值,最终作为该像素的颜色值。
比如说我每个像素sample 1000条光线,如果撞到漫反射表面那就是1000条随机方向的 RayTracing结果的均值,这样便能较为准确的模拟了漫反射表面的特性了。 (对一个像素进行多次sample,其实也就把抗锯齿也给做了)
(tips: 该方法其实更多算是path tracing,经典的whited-style光线追踪遇到漫反射表面会直接利用blinn-phong模型计算颜色值返回,而不再递归下去)
Accelerating Ray-Surface Intersection
为什么
原始:每根光线和每个三角形求交(太慢!)
**轴对齐包围盒 Axis-Aligned Bounding Box (AABB) **

原理
当有的光线显然不会与一个物体相交的时候,那么自然也没有必要去遍历该物体的所有三角形面,因此利用一个包围盒包住该物体,在与该物体的三角面计算求交之前先判断光线是否与包围盒相交,倘若连包围盒都与光线没有交点的话,那么显然不会与物体的三角面有交点。
过程
以2D AABB为例子,因此只有x,y两对平面(二维应该其实是线,不过为了统一性这里依然称为平面,不影响理解),3D情况可类推:
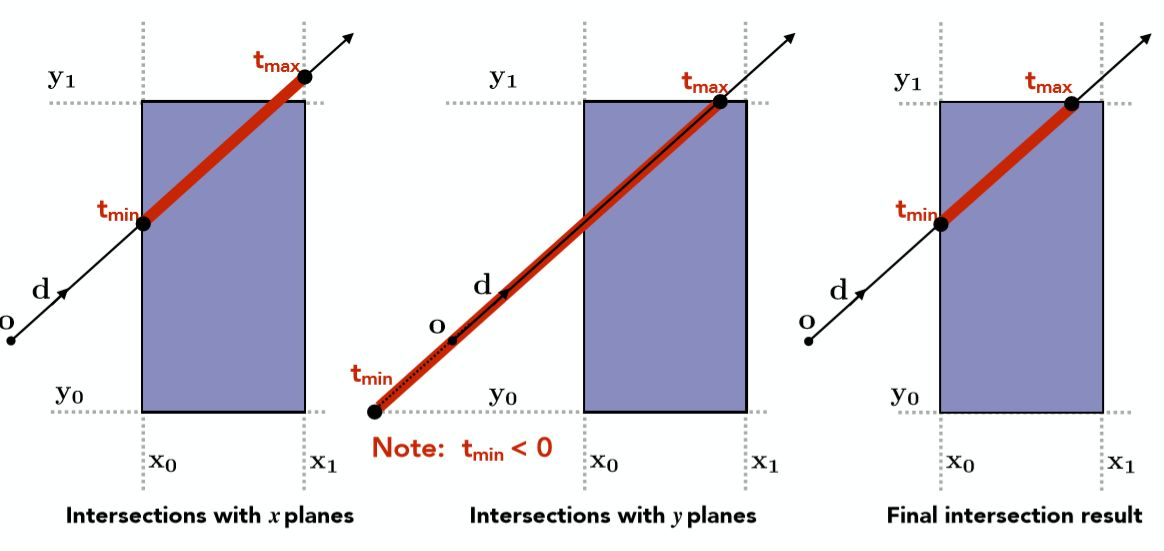
首先如上图最左边所示,求出光线与一对x平面的交点,将先进入的交点(偏小的那个)记为 tmin, 后出去的交点(偏大的那个)记为 tmax,紧接着如中间图所示计算出光线与y平面的两个交点同样记为另外一组tmin, tmax,当然计算的过程中要注意如果任意的 t < 0,那么这代表的是光线反向传播与对应平面的交点。
1 只有当光线进入了所有的平面才算是真正进入了盒子中
2 只要当光线离开了任意平面就算是真正离开了盒子
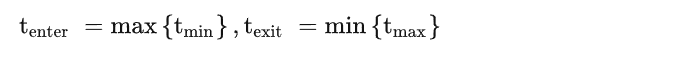
但光线一定会与包围盒有交点吗?显然不是,那么什么条件下才会有交点呢? 我们说当tenter < texit 的时候,光线所在直线一定在盒子中待过一段时间,也必然存在交点,但光线并不是直线,而是射线,除了保证了光线所在的直线在盒子里待过一段时间,还要考虑实际物理意义,具体如下:

带来效率提升
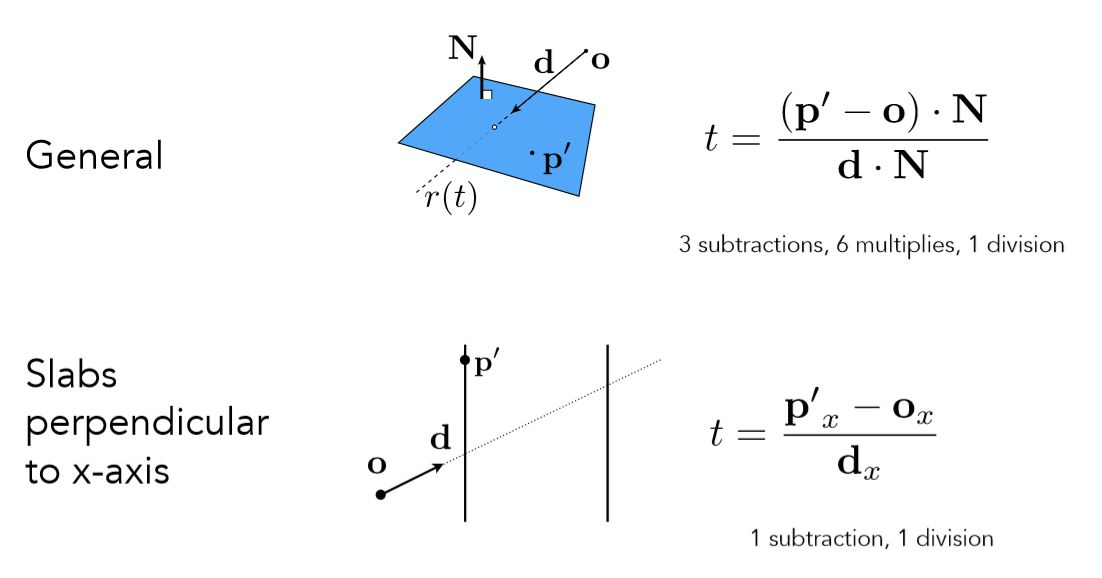
r(t)=o+td=p=p,
=>t
**均匀空间划分 **Uniform Spatial Partitions(Grids)
为什么
考虑以下情况:
整个场景只有一个极其复杂的单一人物模型,那么只对这一个物体做包围盒的话,相当于对效率没有任何提升
整个场景充斥着大量的细小模型,如草,花之类的,每个模型可能只有很少的面,如果此时对每个物体求包围盒,得到的包围盒数量会相当之多,对于光线追踪效率来说效率提升有限
基于以上两点考虑,AABB并不应只局限于以物体模型为单位,可以更加精细的考虑到以三角面为单位。另外对于场景的许许多多包围盒来说应该要有一种数据结构将其统领起来。 因此如何更好的划分场景形成不同的AABB,使得划分之后的AABB能够更好的加速光线追踪,这就是接下来要考虑的问题关键! (以下的划分形成的AABB更是一种general的概念,可能不会严格包围物体)
过程
第一步对所要考虑的场景找一个包围盒:
第二步均匀划分这个大包围盒:
第三步在每个重叠小包围盒上存储物体模型信息
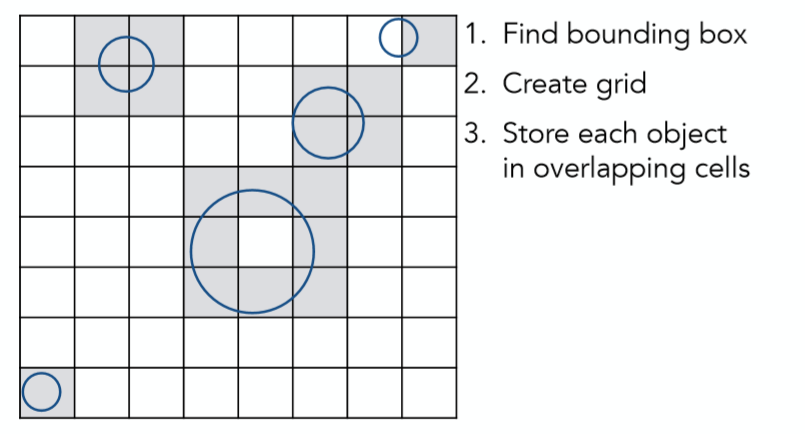
紧接着,根据光线的方向与判断出所有相交的方格(这一步可以利用bresenham算法),倘若方格中存储有物体,再进一步与方格中的物体模型或是三角形面求交。
简单来说就是将空间划分为多个均匀的小的AABB,再根据光线方向找出相交grid(这一步并不需要判断所有方格,正如上文提示,可以用brenham类似的方法来做),再判断grid中是否存储了模型信息,若有则进一步求交。(这种划分方法假设了找出相交方格要比直接判断与物体求交相对容易,因此划分方格数的多少也是性能的关键,方格太少,没有加速效果,方格太多,判断与方格的求交可能会拖累效率)

KD-Tree空间划分
在具体介绍KD-Tree空间划分的方法之前,首先来看看一些常用的空间划分方法:
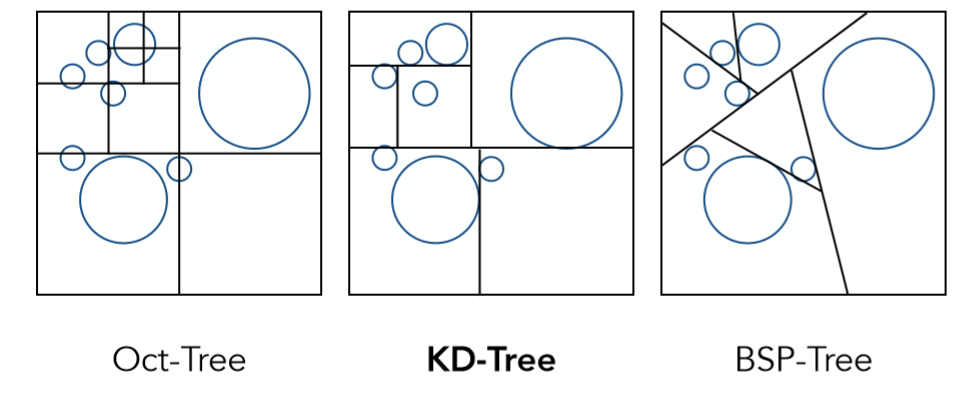
第一种Oct-Tree,也就是八叉树,每次将空间分为8个相等的部分,再递归的对子空间进行划分,因为图中是2维例子,所以只划分了4部分。当划分的子空间足够小或是空间中三角形面的数量很少的时候会停止划分。这种方法的显著缺点是,随着维度的上升划分的空间数量会呈指数级增长。
第二种KD-Tree,也是本小节将要主要介绍的方法,其每次将空间划分为两部分,且划分依次沿着x-axis,y-axis,z-axis,即如图中所示,第一次横着将2维空间分为上下,第二次再竖着将上下两个子空间分别划分为左右部分,依次递归划分,终止条件与八叉树类似,细节问题之后按具体例子详解。
第三种BSP-Tree,其与KD-Tree类似,唯一不同的是划分不再沿着固定一轴,可以任意方向划分,缺点自然是划分的空间没有规则性,求交困难。
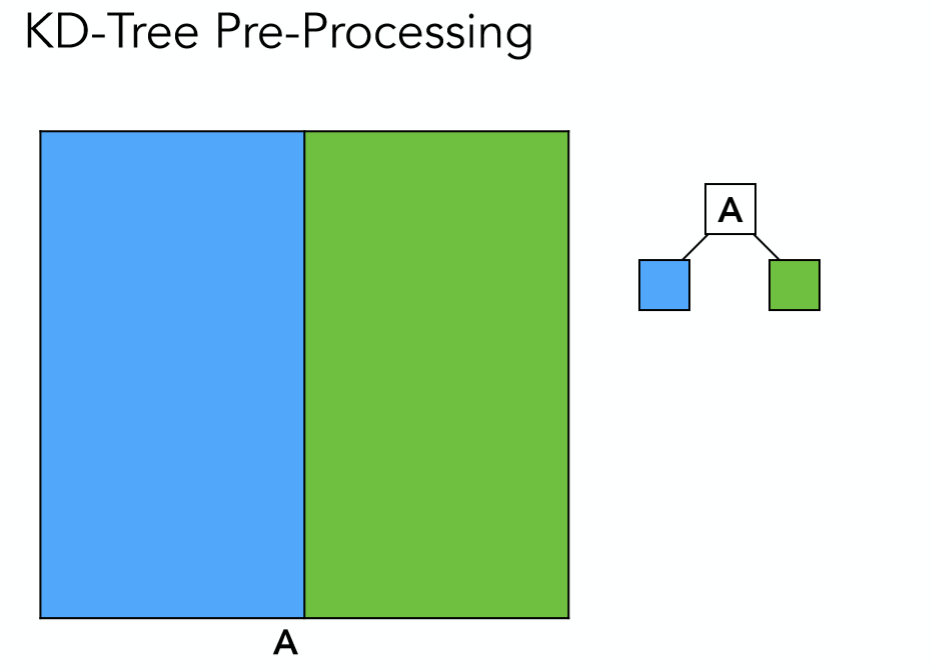
过程
第一步将空间分为两部分
第二步对左右两个子空间换个方向再分为两部分(这里只画出了有半部分,其实左边也是一样)
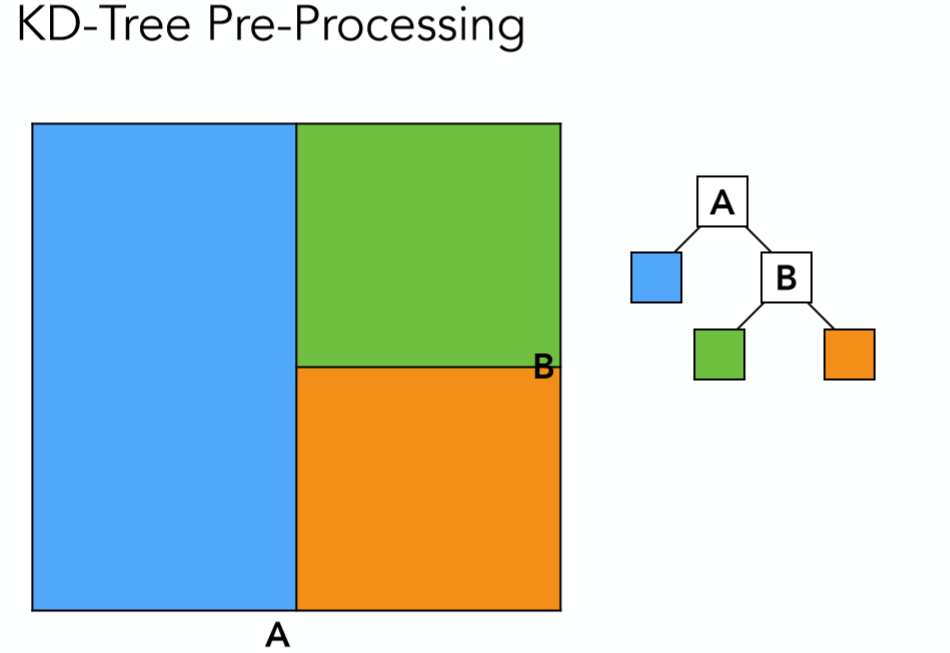
如此递归的划分下去,且在划分过程当中遵循这样几点:
1 依次沿着x-axis,y-axis,z-axis划分,使得空间被划分的更加平衡
2 划分的位置由空间中三角面的分布决定,具体细节不展开
3 叶子节点存储对应空间的所有物体或三角面信息,中间节点仅存储指针指向两个子空间
4 当划分空间太小或是子空间内只有少量三角形则停止划分
当KD-Tree建立完成之后,如何进行光线与物体求交判断呢?过程如下:
第一步判断光线是否与最外层的包围盒相交
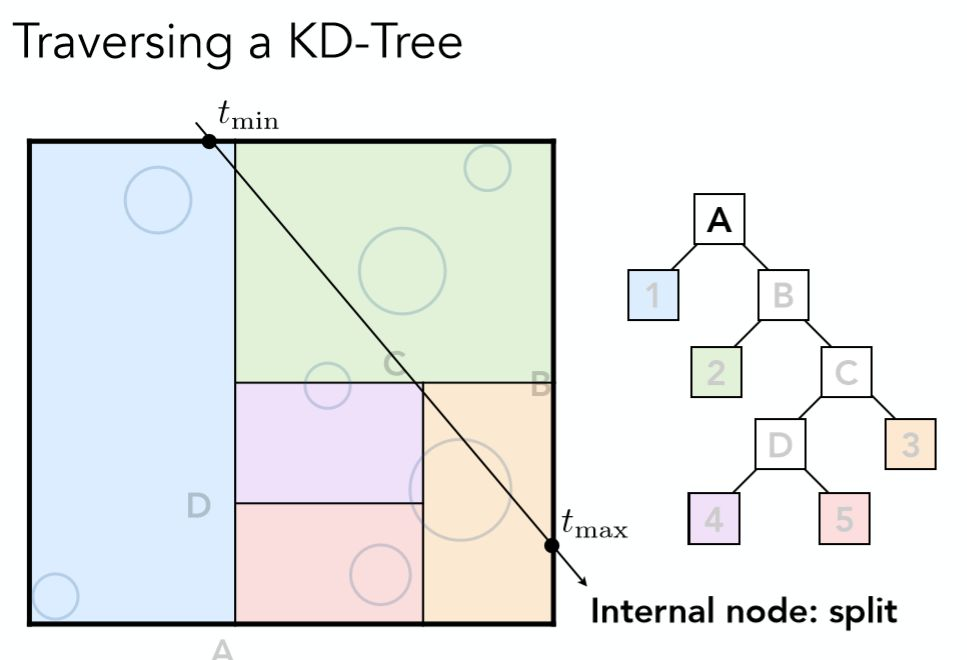
如果相交进一步判断是否与对应的两个子空间相交
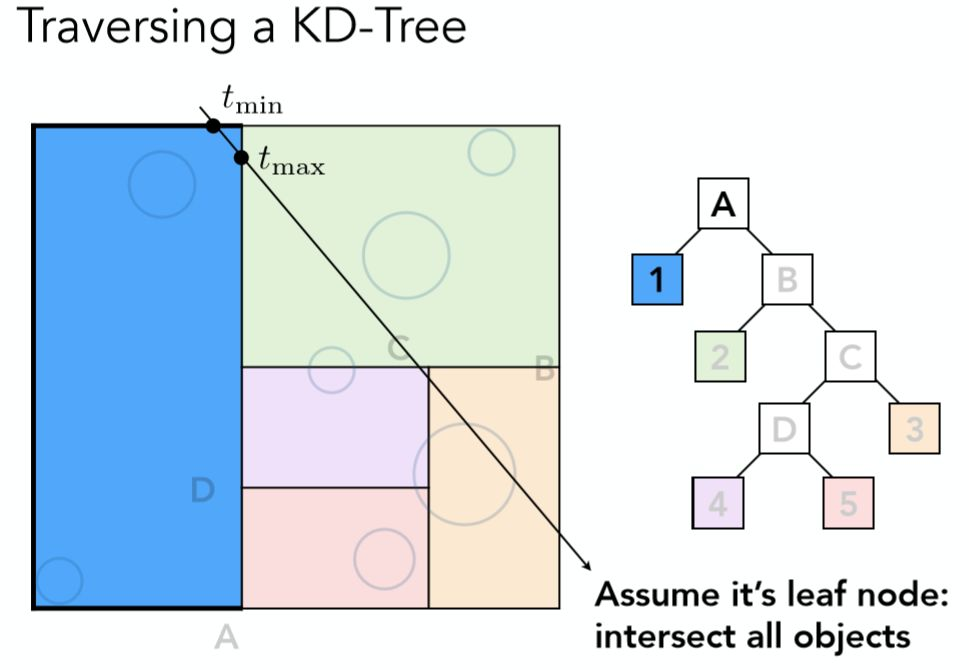
注意!因图中做了简化,最大包围盒的左半边并没继续进行划分(实际上应该要划分的),所以左半部分对应的1号空间是叶子节点,如果光线与之相交,进一步判断与存储与叶子节点的物体信息求交。左半边判断完之后,接着判断右半部分。
优点: 利用KD-Tree的结构来构建AABB的好处是倘若光线与哪一部分空间不相交,那么则可以省略该部分空间所有子空间的判断过程,在原始的纯粹的AABB之上更进一步提升了加速效率。
缺点: 缺点是判断包围盒与三角面的是否相交较难,因此划分的过程不是那么想象的简单,其次同一个三角面可能被不同的包围盒同时占有,这两个不同包围盒内的叶节点会同时存储这一个三角形面
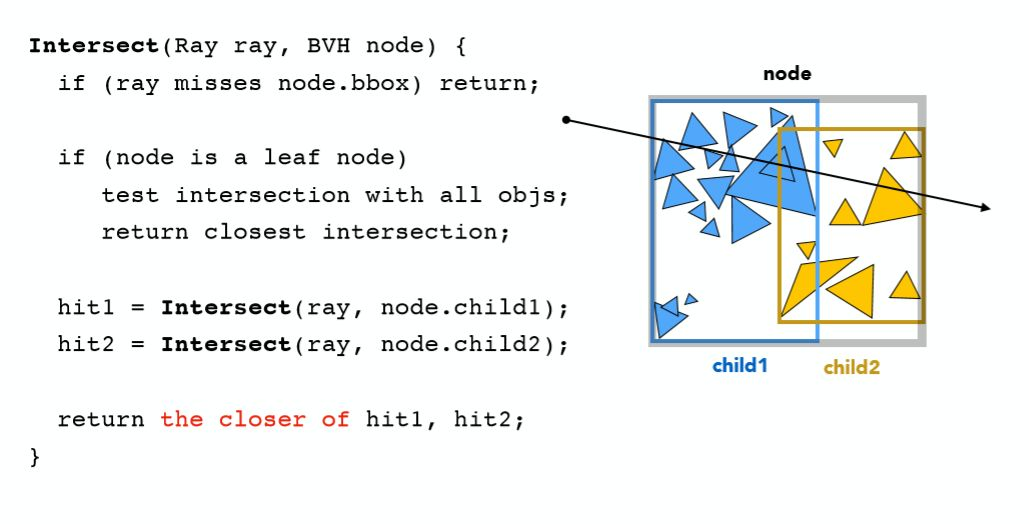
BVH(Bounding Volume Hierarchy)
BVH与前几种方法最显著的区别就是,不再以空间作为划分依据,而是从对象的角度考虑,即三角形面,过程如下: 第一步同样找出场景的整体包围盒作为根节点
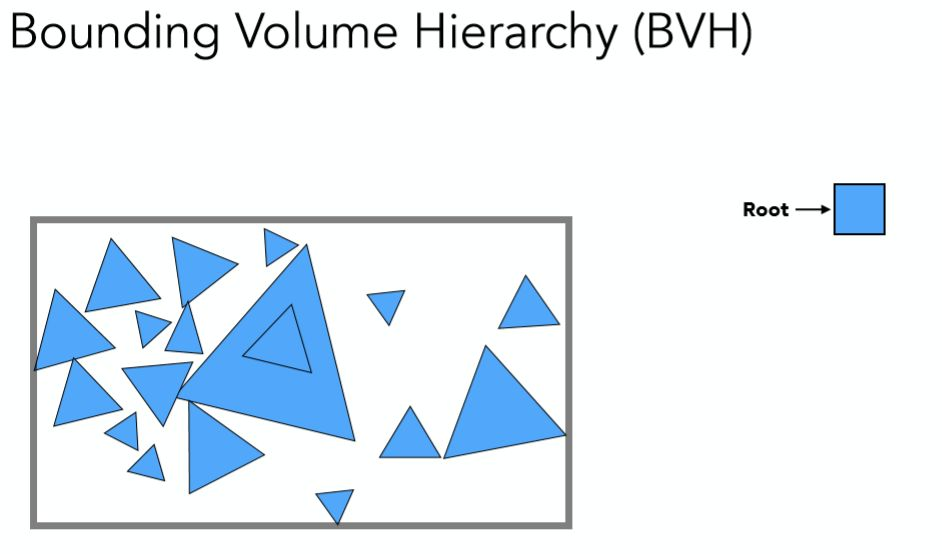
第二步找到合适的划分点,将最大包围盒内的三角形面分为两部分,再分别重新就算新的包围盒
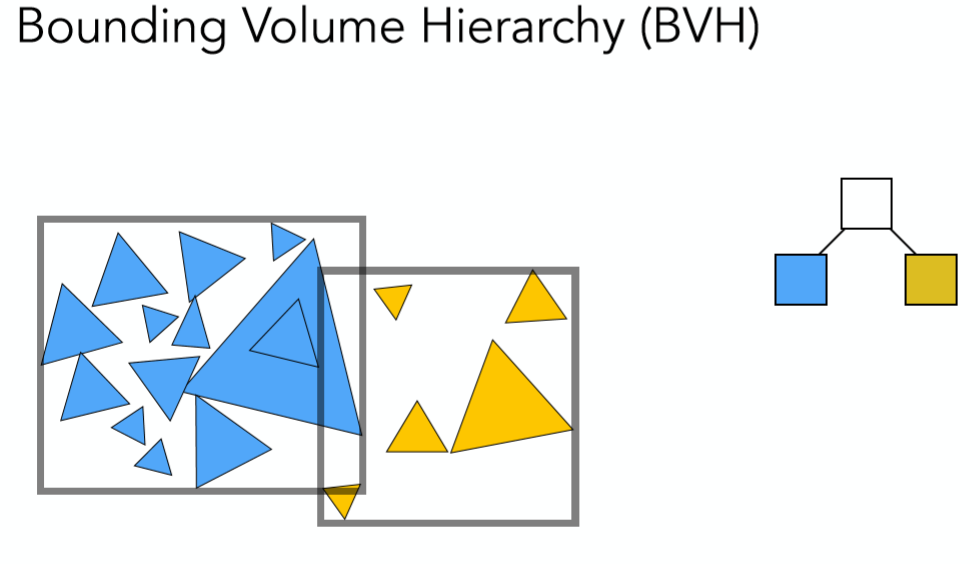
注意到这里,包围盒会重叠,但一个三角形面只会被存储在唯一的包围盒内,而这也就解决了KD-Tree的缺点! 接下来与KD-Tree的建立类似,递归的对所有子空间重复该步骤
tips:
每次划分一般选择最长的那一轴划分,假设是x轴,那么划分点选择所有三角面的重心坐标在x坐标上的中位数进行划分,如此便能保证划分的三角形左右两边三角形数量尽可能差不多,当然也就使得树形结构建立的更加平衡,深度更小,平均搜索次数更少,提高了效率
与KD-Tree一样,中间节点不存储物体三角面信息,只在叶节点中存储,终止条件可设定为当前包围盒内三角形数量足够少 (e.g. 5个)
伪代码: