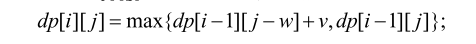动态规划

动态规划

递推求解

错排公式

我们按照 n 的取值顺序将所有的错装方式数量排 列为一个数列，同样用 F[n]表示数列里第 n 个数的取值，F[n]同时代表 n 个信封 的错装方式总数，我们确定该数列的递推关系。当 n 大于 3 时，我们考虑 n 封信 全部装错的情况。将信封按顺序由 1 到 n 编号。在任意一种错装方案中，假设 n 号信封里装的是 k 号信封的信，而 n 号信封里的信则装在 m 号信封里。按照k和m的等值与否将总的错误方式分为两类。

若 k 不等于m，交换 n 号信封和m号信封的信后，n 号信封里装的恰好是对
应的信，而 m 号信封中错装 k 号信封里的信，即除 n 号信封外其余 n-1 个信封 全部错装，其错装方式等于 F[n - 1]，又由于m的 n-1 个可能取值，这类错装方 式总数为（n - 1）* F[n - 1]。也可以理解为，在 n-1 个信封错装的 F[n - 1]种方式 的基础上，将 n 号信封所装的信与n - 1个信封中任意一个信封（共有 n-1 中选 择）所装的信做交换后，得到所有信封全部错装的方式数。

另一种情况，若 k 等于m，交换 n 号信封和m号信封的信后，n 号信封和m 号信封里装的恰好是对应的信，这样除它们之外剩余的 n-2 个信封全部错装，其 错装方式为 F[n - 2]，又由于m的 n-1 个取值，这类错装方式总数为（n - 1）* F[n - 2]。也可以理解为，在 n - 2 个信封全部错装的基础上，交换最后两个信封中的 信(n 号信封和 1 到 n-1 号信封中任意一个，共有 n-1 种选择)，使所有的信封全部 错装的方式数。

综上所述，F[n] = (n - 1) * F[n - 1] + (n - 1) * F[n - 2]。这就是有名的错排公式

主要代码

1
2
3
4
5
F[1]=0;
F[2]=1;
for(int i=3;i<=20;i++)
    F[i]=(i-1)*F[i-1]+(i-1)*F[i-2];
    //递推求得数列的每一个数字

最长递增子序列 LIS

原理

示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<cmath>
using namespace std;
int dp[26];
int a[26];
int main()
{
    int k;
    while(cin>>k&&k)
    {
        for(int i=1;i<=k;i++)
        cin>>a[i];
        
        for(int i=1;i<=k;i++)
        {
            int tmax=1;
            for(int j=1;j<i;j++)
                if(a[j]>=a[i])
                    tmax=max(tmax, dp[j]+1);
            dp[i]=tmax; 
        }

        int ans=1;
        for(int i=1;i<=k;i++)
        {
            ans=max(ans,dp[i]);
        }
        cout<<ans<<endl;
    }
    
}

示例2

思路：

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<iostream>
#include<cmath>
using namespace std;
int dp1[101];
int dp2[101];
int a[101];
int main()
{
    int N;
    while(cin>>N)
    {
        for(int i=1;i<=N;i++)
            cin>>a[i];
        for(int i=1;i<=N;i++)
        {
            dp1[i]=1;
            for(int j=1;j<i;j++)
            {
                if(a[i]>a[j])
                    dp1[i]=max(dp1[i],dp1[j]+1);
            }
        }
        
        for(int i=N;i>=1;i--)
        {
            dp2[i]=1;
            for(int j=N;j>i;j--)
            {
                if(a[i]>a[j])
                   dp2[i]=max(dp2[i],dp2[j]+1);
            }
        }
        int ans=0;
        for(int i=1;i<=N;i++)
        {
            ans=max(ans,dp1[i]+dp2[i]);
        }
        cout<<N-ans+1<<endl;
    }
    return 0;
}

最长公共子序列(LCS)

有两个字符串 S1 和 S2，求一个最长公共子串，即求字符串 S3，它同时为
S1 和 S2 的子串，且要求它的长度最长，并确定这个长度。这个问题被我们称为 最长公共子序列问题

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<iostream>
#include<string>
#include<cmath>
using namespace std;
int dp[101][101];//dp[i][j]  i,j代表长度为i，j的字符串
int main()
{
    string a,b;
    while(cin>>a>>b)
    {
        int lena=a.length();
        int lenb=b.length();
        
        for(int i=0;i<=lena;i++)
            for(int j=0;j<=lenb;j++)
            {
                if(i==0||j==0) {
                    dp[i][j]=0;
                    continue;
                }
                if(a[i-1]==b[j-1]) dp[i][j]=dp[i-1][j-1]+1;
                else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
               
            }
        cout<<dp[lena][lenb]<<endl;
    }
    return 0;
}

动态规划问题分析举例

搬寝室


示例代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <iostream>
#include <algorithm>
using namespace std;
const int INF = 0x7fffffff; //预定义最大的int取值为无穷
int list[2001];             //保存每个物品重量
int dp[1001][2001];         //保存每个状态
int main()
{
    int n, k;
    while (cin >> n >> k && n && k)
    {
        for (int i = 1; i <= n; i++)
            cin >> list[i];
        sort(list + 1, list + 1 + n); //使所有物品按照重量递增排序
        for (int i = 1; i <= n; i++)
            dp[0][i] = 0;
        for (int i = 1; i <= k; i++)
        {
            //递推求得每个状态
            for (int j = 2 * i; j <= n; j++)
            {
                if (j > 2 * i)
                    dp[i][j] = dp[i][j - 1];
                //j>2*i表明，最后两个物品可以不配对，即前j-1件物品足够配成i对
                //dp[i][j]可以由dp[i][j - 1]转移而来，其值先被设置为dp[i][j - 1]
                else
                    dp[i][j] = INF;
                //若j==2*i，说明最后两件物品必须配对，否则前j件物品配不成i对，
                //所有其状态不能由dp[i][j-1]转移而来，dp[i][j]先设置为正无穷
                if(  dp[i][j]> (dp[i-1][j-2]+(list[j]-list[j-1])*(list[j]-list[j-1]))  )
                {
                    //若dp[i][j]从dp[i-1][j-2]转移而来时，其值优于之前确定的正无穷
                    //或者由dp[i][j-1]转移而来的值时，更新该状态
                    dp[i][j] = dp[i - 1][j - 2] + (list[j] - list[j - 1]) * (list[j] - list[j - 1]); //更新
        
                }
            }
        }
        cout << dp[k][n] << endl;
    }
    return 0;
}

背包问题

主要讨论0-1背包，完全背包和多重背包三类问题

0-1背包问题

采药

首先我们将这个问题抽象：有一个容量为 V 的背包，和一些物品。
这些物品分别有两个属性，体积w和价值 v，每种物品只有一个。
要求用这个背包装下价值尽可能多的物品，求该最大价值，背包可以不被装满。
因为最优解中，每个物品都有两种可能的情况，即在背包中或者不存在（背
包中有 0 个该物品或者 1 个），所以我们把这个问题称为 0-1 背包问题。在该例 中，背包的容积和物品的体积等效为总共可用的时间和采摘每个草药所需的时间。

在众多方案中求解最优解，是典型的动态规划问题。为了用动态规划来解决
该问题，我们用 dp[i][j]表示在总体积不超过 j 的情况下，前 i 个物品所能达到的 最大价值。

初始时，dp[0][j] (0<=j<=V)为 0。依据每种物品是否被放入背包，每个状态有两个状态转移的来源。

若物品 i 被放入背包，设其体积为w，价值为 v， 则 dp[i][j] = dp[i - 1][j - w] + v。即在总体积不超过 j-w 时前 i-1 件物品可组成的最大价值的基础上再加上i物品的价值v；

若物品不加入背包，则dp[i][j] = dp[i-1][j]， 即此时与总体积不超过 j 的前 i-1 件物品组成的价值最大值等价。

选择它们之中 较大的值成为状态 dp[i][j]的值。

综上所述，0-1 背包的状态转移方程为：

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
#include<cmath>
using namespace std;
struct Node{
    int w;
    int v;
}a[101];
int dp[101][1001];//dp[i][j]表示前i个物品组成的总体积不大于j的最大价值和
int main()
{
    int V,M;
    while(cin>>V>>M)
    {
        for(int i=1;i<=M;i++)
            cin>>a[i].v>>a[i].w;
        for(int i=1;i<=V;i++) //初始化
            dp[0][i]=0;
        for(int i=1;i<=M;i++) //循环遍历每个物品
        {
            for(int j=V;j>=a[i].v;j--)
            {
                dp[i][j]=max(dp[i-1][j],dp[i-1][j-a[i].v]+a[i].w);
            }
            for(int j=a[i].v-1;j>=0;j--)
                dp[i][j]=dp[i-1][j];
        }
        cout<<dp[M][V]<<endl;
    }
    return 0;
}

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
using namespace std;
const int INF=0x7fffffff;
int max(int a,int b){
    return a>b?a:b;
}
struct E{
    int w;//物品的体积
    int v;//物品的总价值
}list[101];
int dp[1001];//dp[i][j]表示前i个物品组成的总体积不大于j的最大价值和
int main()
{
    int s,n;
    while(cin>>s>>n){
        for(int i=1;i<=n;i++)
          cin>>list[i].w>>list[i].v;
        for(int i=0;i<=s;i++){
            dp[i]=0;//初始化状态
        }
        for(int i=1;i<=n;i++){
            //循环每一个物品
            for(int j=s;j>=list[i].w;j--){
                //对s到list[i].w的每个j，状态转移来源为dp[i-1][j]
                //或dp[i-1][j-list[i].w]+list[i].v,选择其中较大的值
                dp[j]=max(dp[j],dp[j-list[i].w]+list[i].v);
            }
        }
        cout<<dp[s]<<endl;
    }
    return 0;
}

完全背包问题

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<iostream>
#include<cmath>
using namespace std;
const int INF=0x7fffffff;

struct E{//钱币结构体
    int w;//重量
    int v;//价值
}list[501];
int dp[10001];//状态
int main()
{
    int T;
    cin>>T;//输入测试数据组数
    while(T--)
    {
        //T次循环，处理T组数据
        int s,tmp;
        cin>>tmp>>s;//输入空储蓄罐重量和装满钱币的储蓄罐重量
        s-=tmp;//计算钱币所占重量
        int n;
        cin>>n;
        for(int i=1;i<=n;i++)
        {
            cin>>list[i].v>>list[i].w;//输入不同种类钱币的价值和重量
        }
        //因为是要求正好相等  所以初始时，除dp[0]外，其余dp[j]设置初始值为无穷或不存在
        for(int i=0;i<=s;i++)
            dp[i]=INF;
        dp[0]=0;

        for(int i=1;i<=n;i++){//遍历所有物品
           for(int j=list[i].w;j<=s;j++){
               //完全背包，顺序遍历所有可能转移的状态
               if(dp[j-list[i].w]!=INF) //若不为无穷，就可以由此状态转移而来
                   dp[j]=min(dp[j],dp[j-list[i].w]+list[i].v);//取转移值和原值的较小值
           }
        }
        if(dp[s]!=INF) //若存在一种方案使背包恰好装满，输出其最小值
            cout<<dp[s]<<endl;
        else
            cout<<"impossible"<<endl;
    }
    return 0;
}

多重背包


输入

1
2
3
4
1
8 2 
2 100 4
4 100 2

输出

1
400

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<iostream>
#include<cmath>
using namespace std;
struct E{//大米
   int w;//价格
   int v;//重量
}list[2001];
int dp[101];
int main()
{
    int T;
    cin>>T;
    while(T--) //T组测试用例
    {
        int s,n;   //经费和大米种类
        cin>>s>>n;
        int cnt=0;
        for(int i=1;i<=n;i++){
            int v,w,k;//价格，重量，袋数
            cin>>v>>w>>k;
            int c=1;
            while(k-c>0){
                //对输入的数字k，拆分成1,2,4，..k-2^c+1,其中c为使最后一项大于0的最大整数
                k-=c;
                list[++cnt].w=c*w;
                list[cnt].v=c*v;//拆分后的大米重量和价格均为组成该物品的大米的重量价格和
                c*=2;
            }
            list[++cnt].w=w*k;
            list[cnt].v=v*k;
        }
        for(int i=1;i<=s;i++) dp[i]=0;//初始值
        for(int i=1;i<=cnt;i++){
            //对拆分后的所有物品进行0-1背包
            for(int j=s;j>=list[i].v;j--){
                dp[j]=max(dp[j],dp[j-list[i].v]+list[i].w);
            }
        }
        cout<<dp[s]<<endl;
    }
    return 0;
}

算法
#总结 #算法
动态规划
https://shanhainanhua.github.io/2021/03/09/动态规划/
作者
wantong
发布于
2021年3月9日
许可协议