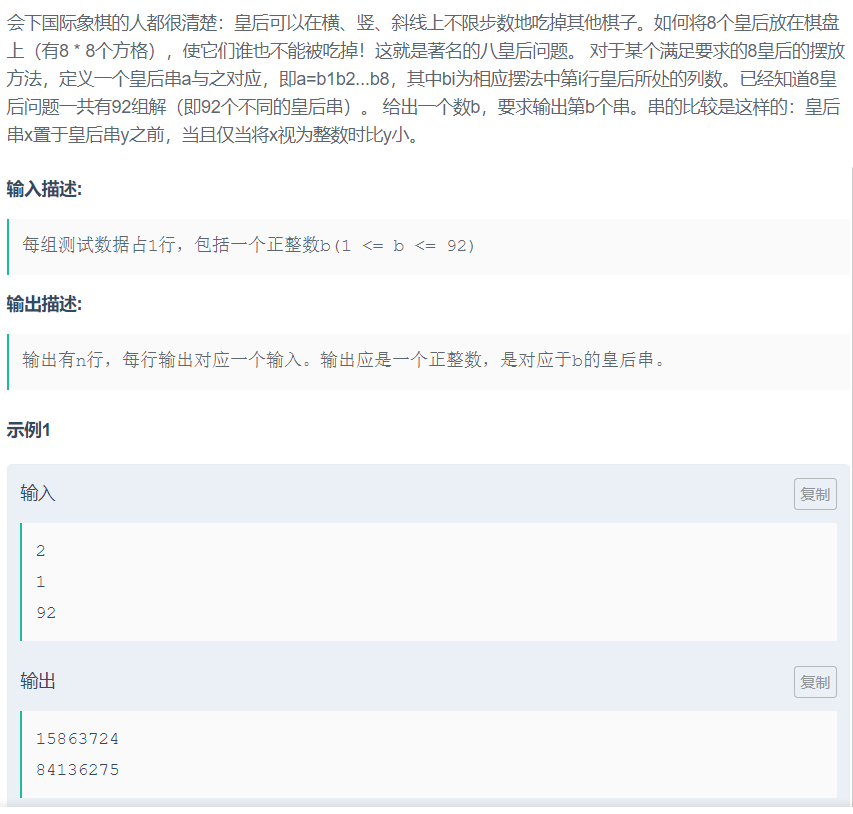
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
|
using namespace std;
struct N{
int a,b,c;//每个杯子中可乐的体积
int t;//得到该体积组倾倒次数
};
queue<N> Q;//队列
bool mark[101][101][101];
void AtoB(int &a,int sa,int &b,int sb)
{
//倾倒函数,由容积为sa的杯子倒往容积为sb的杯子
//a,b,初始时为原始杯子中可乐的体积,
//函数调用完毕后,为各自杯子中可乐的新体积
if(sb-b>=a)
{
//若a可以全部倒到b中
b+=a;
a=0;
}
else
{
a-=sb-b;
b=sb;
}
}
int BFS(int s,int n,int m)
{
while(!Q.empty())
{
N now=Q.front();//拿出队头状态
Q.pop();
int a,b,c;//a,b,c临时保存三个杯子中可乐体积
//可能的状态 a->b
a=now.a;
b=now.b;
c=now.c;
AtoB(a,s,b,n);//由a倾倒向b
if(mark[a][b][c]==false)
{
//若该体积组尚未出现
mark[a][b][c]=true;//标记该体积组
N tmp;
tmp.a=a;
tmp.b=b;
tmp.c=c;
tmp.t=now.t+1;//生成新的状态
if(a==s/2&&b==s/2) return tmp.t;
if(c==s/2&&b==s/2) return tmp.t;
if(a==s/2&&c==s/2) return tmp.t;
//若该状态已经为平分状态,则直接返回该状态的耗时
Q.push(tmp);//否则放入队列
}
//可能的状态b->a
a=now.a;
b=now.b;
c=now.c;
AtoB(b,n,a,s);//由b倾倒向a
if(mark[a][b][c]==false)
{
//若该体积组尚未出现
mark[a][b][c]=true;//标记该体积组
N tmp;
tmp.a=a;
tmp.b=b;
tmp.c=c;
tmp.t=now.t+1;//生成新的状态
if(a==s/2&&b==s/2) return tmp.t;
if(c==s/2&&b==s/2) return tmp.t;
if(a==s/2&&c==s/2) return tmp.t;
//若该状态已经为平分状态,则直接返回该状态的耗时
Q.push(tmp);//否则放入队列
}
//可能的状态a->c
a=now.a;
b=now.b;
c=now.c;
AtoB(a,s,c,m);//由a倾倒向c
if(mark[a][b][c]==false)
{
//若该体积组尚未出现
mark[a][b][c]=true;//标记该体积组
N tmp;
tmp.a=a;
tmp.b=b;
tmp.c=c;
tmp.t=now.t+1;//生成新的状态
if(a==s/2&&b==s/2) return tmp.t;
if(c==s/2&&b==s/2) return tmp.t;
if(a==s/2&&c==s/2) return tmp.t;
//若该状态已经为平分状态,则直接返回该状态的耗时
Q.push(tmp);//否则放入队列
}
//可能的状态 c->a
a=now.a;
b=now.b;
c=now.c;
AtoB(c,m,a,s);//由c倾倒向a
if(mark[a][b][c]==false)
{
//若该体积组尚未出现
mark[a][b][c]=true;//标记该体积组
N tmp;
tmp.a=a;
tmp.b=b;
tmp.c=c;
tmp.t=now.t+1;//生成新的状态
if(a==s/2&&b==s/2) return tmp.t;
if(c==s/2&&b==s/2) return tmp.t;
if(a==s/2&&c==s/2) return tmp.t;
//若该状态已经为平分状态,则直接返回该状态的耗时
Q.push(tmp);//否则放入队列
}
//可能的状态 b->c
a=now.a;
b=now.b;
c=now.c;
AtoB(b,n,c,m);//由b倾倒向c
if(mark[a][b][c]==false)
{
//若该体积组尚未出现
mark[a][b][c]=true;//标记该体积组
N tmp;
tmp.a=a;
tmp.b=b;
tmp.c=c;
tmp.t=now.t+1;//生成新的状态
if(a==s/2&&b==s/2) return tmp.t;
if(c==s/2&&b==s/2) return tmp.t;
if(a==s/2&&c==s/2) return tmp.t;
//若该状态已经为平分状态,则直接返回该状态的耗时
Q.push(tmp);//否则放入队列
}
//可能的状态c->b
a=now.a;
b=now.b;
c=now.c;
AtoB(c,m,b,n);//由c倾倒向b
if(mark[a][b][c]==false)
{
//若该体积组尚未出现
mark[a][b][c]=true;//标记该体积组
N tmp;
tmp.a=a;
tmp.b=b;
tmp.c=c;
tmp.t=now.t+1;//生成新的状态
if(a==s/2&&b==s/2) return tmp.t;
if(c==s/2&&b==s/2) return tmp.t;
if(a==s/2&&c==s/2) return tmp.t;
//若该状态已经为平分状态,则直接返回该状态的耗时
Q.push(tmp);//否则放入队列
}
}
return -1;
}
int main()
{
int s,n,m;
while(cin>>s>>n>>m&&s&&n&&m)
{
if(s%2==1) {
//若s为奇数不可能平分,直接输出NO
cout<<"NO"<<endl;
continue;
}
for(int i=0;i<=s;i++)
for(int j=0;j<=n;j++)
for(int k=0;k<=m;k++)
mark[i][j][k]=false;
//初始化状态
N tmp;
tmp.a=s;
tmp.b=0;
tmp.c=0;
tmp.t=0;
while(!Q.empty()) Q.pop();
Q.push(tmp);//将初始状态放入队列
mark[s][0][0]=true;//标记初始状态
int rec=BFS(s,n,m);//广度优先搜索
if(rec==-1) cout<<"NO"<<endl;
else cout<<rec<<endl;
}
return 0;
}
|