算法之数学问题

涉及机试中涉及的一系列数学问题，包括数位拆解、分解素因数等高频知识点，以及最小公倍数，最大公约数的基本方法，高精度整数运算的实现。

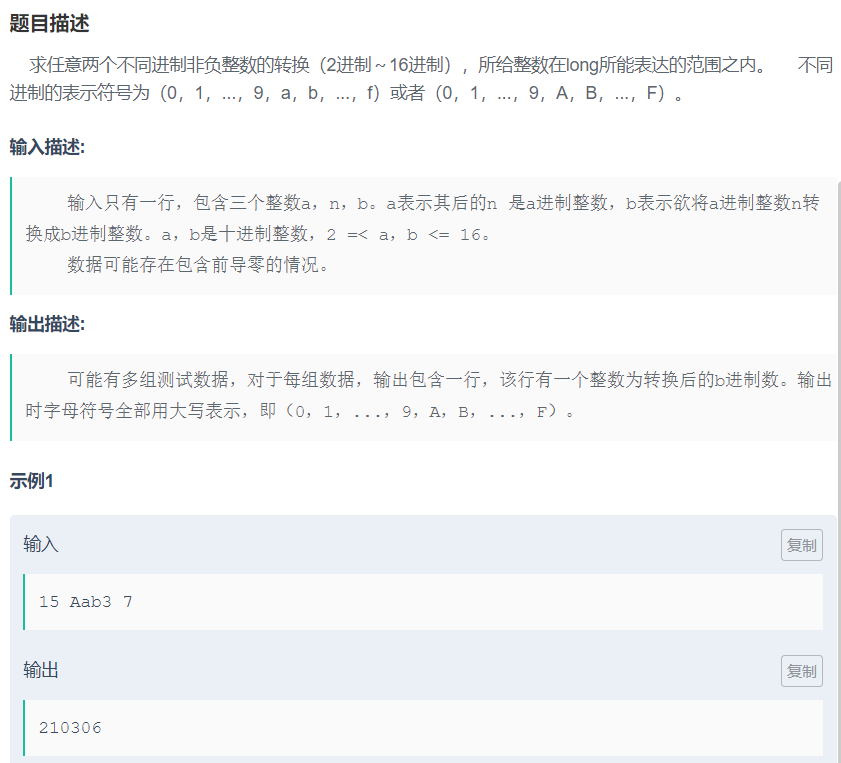
进制转换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <bits/stdc++.h>
using namespace std;
int main()
{
    int a,b;
    string n;
    while(cin>>a>>n>>b)
    {
        long num=0;
        string result="";
        while(n[0]=='0')
            n=n.substr(1);
        int k=1;
        for(int i=n.length()-1;i>=0;--i)
        {
            if(n[i]>='0'&&n[i]<='9')
                num+=(n[i]-'0')*k;
            else if(n[i]>='a'&&n[i]<='z')
                num+=(n[i]-'a'+10)*k;
            else if(n[i]>='A'&&n[i]<='Z')
                num+=(n[i]-'A'+10)*k;
            k*=a;
        }
        while(num!=0)
        {
            if(num%b<=9)
                result=to_string(num%b)+result;
            else
                result=string(1,num%b-10+'A')+result;
            num/=b;
        }
        cout<<result<<endl;
    }
    return 0;
}

最大公约数 GCD

求a,b的最大公约数：

  1. 如果a,b全为0，则它们的最大公约数不存在
  2. 若a,b其中之一为零，它们的最大公约数为a,b中非0的那个
  3. 若a,b都不为0 则使a=b;b=a%b; 然后重复该过程
1
2
3
4
5
int gcd(int a,int b)
{   
    if(b==0) return a;
    else return gcd(b,a%b);
}

最小公倍数 LCM

a,b两数的最小公倍数为两数的乘积除以它们的最大公约数

素数

合数是指在大于1的整数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。与之相对的是质数（素数），而1既不属于质数也不属于合数。最小的合数是4。其中，完全数与相亲数是以它为基础的。

素数筛

若一个数不是素数，则必存在一个小于它的素数为其的因数。在我们获得一个素数时，将它的所有倍数均标记为非素数，这样当我们遍历到一个数时，它没有被任何小于它的素数标记为非素数，则确定其为素数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#include<iostream>
using namespace std;
int prime[10000]={0};
int primesize=0;
bool mark[10001];
void init()
{
    for(int i=1;i<10001;i++)
        mark[i]=false;
    for(int i=2;i<=10000;i++){
        if(mark[i]==true)
            continue;
        prime[primesize++]=i;
        for(int j=i*i;j<=10000;j+=i)
            mark[j]=true;
    }
}
int main()
{
    init();
    int n;
    while(cin>>n)
    {
        bool flag=false;
        for(int i=0;i<primesize;i++)
        {
            if(prime[i]<n&&prime[i]%10==1)
            {
                if(flag==false)
                {
                    flag=true;
                    cout<<prime[i];
                }
                else{
                    cout<<" "<<prime[i];
                }
            } 
        }
        cout<<endl;
    }
    return 0;
}

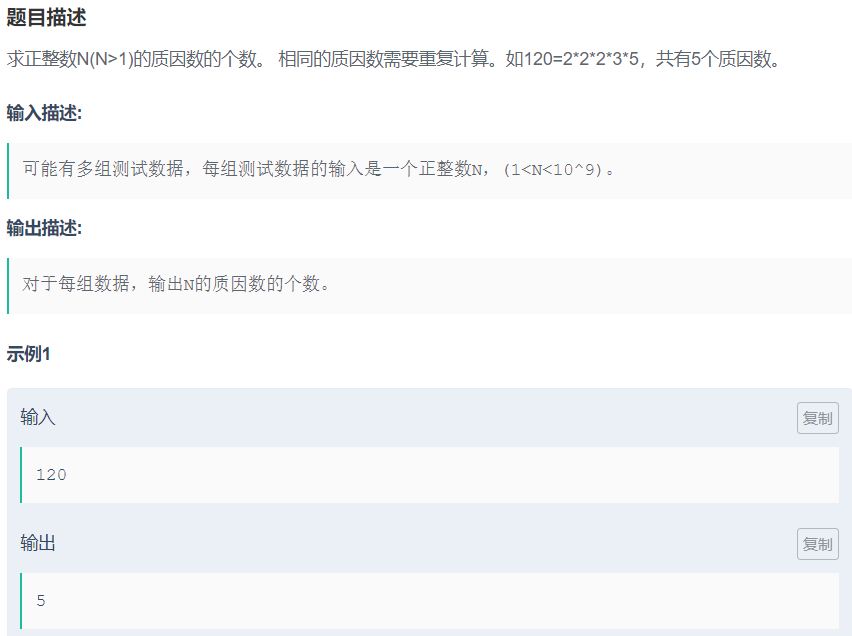
分解素因数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<iostream>
using namespace std;
int prime[100000]={0};
int primesize;
bool mark[100001];
void init()
{
    for(int i=0;i<100001;i++)
        mark[i]=false;
    for(int i=2;i<=100000;i++)
    {
        if(mark[i])
            continue;
        prime[primesize++]=i;
        for(int j=i*i;j<=100000;j+=i)
            mark[j]=true;
    }
}
int main()
{
    init();
    int N;
    while(cin>>N)
    {
         int ansPrime[30];//按顺序保存分解出的素因数
         int ansSize=0;//分解出素因数的个数
         int ansNum[30]; //保存分解出的素因数对应的幂指数
        for(int i=0;i<primesize;i++)
        {
            if(N%prime[i]==0){ //若该素数能整除分解数
                ansPrime[ansSize]=prime[i];//则该素数为其素因数
                ansNum[ansSize]=0;//初始化幂指数为0
                while(N%prime[i]==0)
                {
                    ansNum[ansSize]++;
                    N/=prime[i];
                }
                ansSize++;
                if(N==1) break;
            }
        }
        if(N!=1){
            ansPrime[ansSize]=N;//若测试所有素因数，n仍未被分解至1，则剩余的因数一定是N一个大于100000的素因数
            ansNum[ansSize++]=1;
        }
        int ans=0;
        for(int i=0;i<ansSize;i++){
            ans+=ansNum[i]; 
        }
        cout<<ans<<endl;
        
    }
    return 0;
}

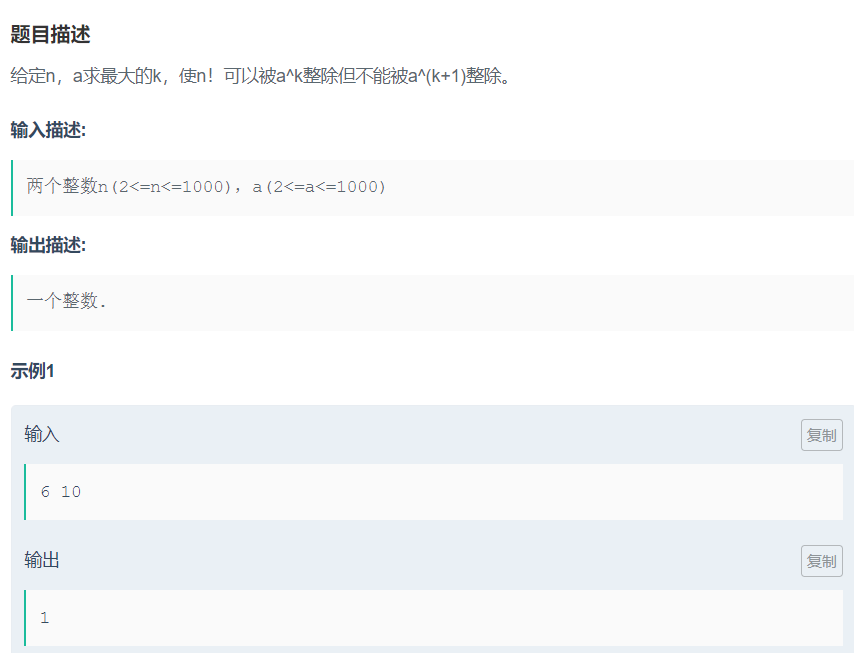
阶乘的素因数分解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<stdio.h>
int main(){
    int a,n;
    while(scanf("%d%d",&n,&a)!=EOF){
        int count1[1010]={0};
        int count2[1010]={0};
        for(int i=2;i<=n;i++){
            int t=n;
            while(t){
                count1[i]+=t/i;
                t=t/i;
            }
        }
        int ans=233333333;
        for(int i=2;i<=a;i++){
            while(a%i==0){
                count2[i]++;
                a/=i;
            }
            if(count2[i]==0) continue;
            if(count1[i]/count2[i]<ans)
                ans=count1[i]/count2[i];
        }
        printf("%d\n",ans);
    }
    return 0;
}

使用素数筛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include<stdio.h>
#define N 1010
int prime[N];
int primesize;
bool mark[N];
void init(){
    for(int i=0;i<N;i++)
        mark[i]=false;
    for(int i=2;i<N;i++){
        if(mark[i]==true) continue;
        else{
            prime[primesize++]=i;
            for(int j=i*i;j<N;j+=i)
                mark[j]=true;
        }
    }
}
int main(){
    init();
    int a,n;
    while(scanf("%d%d",&n,&a)!=EOF){
        int count1[N]={0};
        int count2[N]={0};
        for(int i=0;i<primesize;i++){
            int t=n;
            while(t){
                count1[i]+=t/prime[i];
                t/=prime[i];
            }
        }
        int ans=233333333;
        for(int i=0;i<primesize;i++){
            while(a%prime[i]==0){
                count2[i]++;
                a/=prime[i];
            }
            if(count2[i]==0) continue;
            if(count1[i]/count2[i]<ans)
                ans=count1[i]/count2[i];
        }
        printf("%d\n",ans);
    }
    return 0;
}

二分求幂

快速幂

csdn相关介绍博客

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<iostream>
using namespace std;
int binaryPow(int a,int b)
{
    int ans=1;
    while(b)
    {
        if(b%2!=0)  //对应二进制位为1  可以写成b&1 取二进制最后一位
           ans*=a;  //累乘至结果
        a*=a;       //准备
        b/=2;       //可以写成b>>1
    }
    return ans;
}
int main()
{
    int a,b;
    while(cin>>a>>b)
    {
       cout<<binaryPow(a,b)<<endl;
    }
    return 0;
}

矩阵快速幂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
const int N=10;
int tmp[N][N];
void multi(int a[][N],int b[][N],int n)
{
    memset(tmp,0,sizeof tmp);
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
        for(int k=0;k<n;k++)
        tmp[i][j]+=a[i][k]*b[k][j];
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
        a[i][j]=tmp[i][j];
}
int res[N][N];
void Pow(int a[][N],int n)
{
    memset(res,0,sizeof res);//n是幂，N是矩阵大小
    for(int i=0;i<N;i++) res[i][i]=1;
    while(n)
    {
        if(n&1)
            multi(res,a,N);//res=res*a;复制直接在multi里面实现了；
        multi(a,a,N);//a=a*a
        n>>=1;
    }

————————————————
版权声明：本文为CSDN博主「wust_wenhao」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
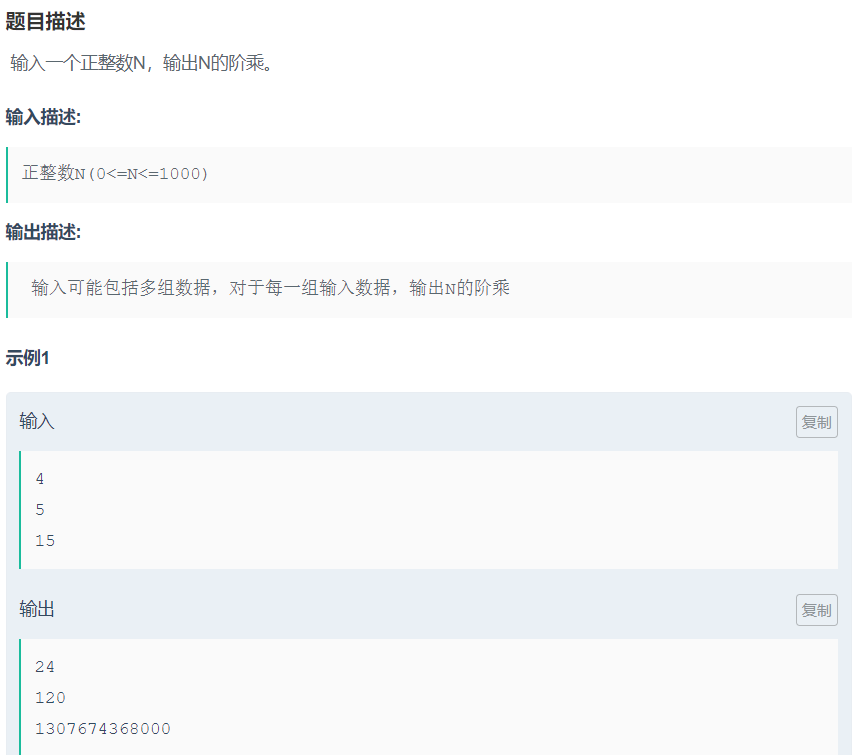
原文链接：https://blog.csdn.net/wust_zzwh/article/details/52058209

高精度整数

计算n的阶乘

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<iostream>
using namespace std;
int res[3000]={0};
int main()
{
    int N;
    while(cin>>N)
    {
        for(int i=0;i<3000;i++) res[i]=0;
        int size=0;res[size++]=1;
        for(int i=2;i<=N;i++)
        {
            int jinwei=0;
            for(int j=0;j<size;j++)
            {
                res[j]=(res[j]*i+jinwei);
                if(res[j]>9)
                {
                    jinwei=res[j]/10;
                    res[j]%=10;
                }     
                else jinwei=0;
            }
            while(jinwei){
                res[size++]=jinwei%10;
                jinwei/=10;
            }
        }
        for(int i=size-1;i>=0;i--)
            cout<<res[i];
        cout<<endl;
    }
    return 0;
}
算法
#总结 #算法
算法之数学问题
https://shanhainanhua.github.io/2021/03/01/算法之数学问题/
作者
wantong
发布于
2021年3月1日
许可协议