数据结构相关算法

包含树，图，bfs，dfs，最短路径，最小生成树等常用模版代码

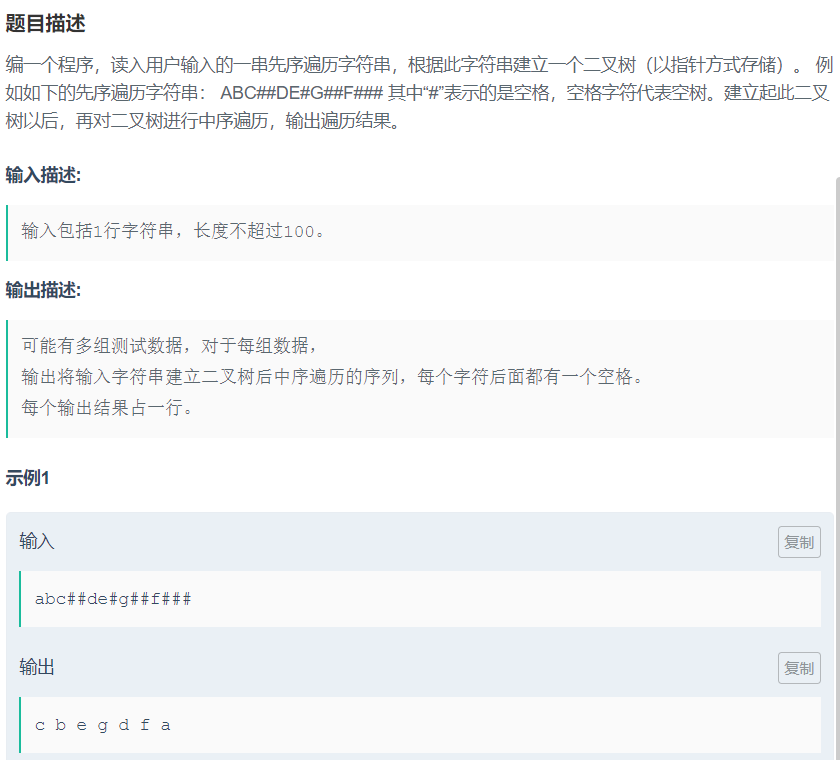
二叉树

题目1：遍历二叉树

  1. 利用结论：二叉树的先序遍历入栈，那么出栈顺序就是他的中序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
#include <string>
#include <stack>
using namespace std;
int main()
{
    string pre;
    while (cin >> pre)
    {
        stack<char> s;
        for (auto it : pre)
        {
            if (it != '#')
                s.push(it);
            else
            {
                if (!s.empty())
                {
                    cout << s.top() << ' ';
                    s.pop();
                }
            }
        }
        cout << '\n';
    }
}

  1. 使用数组模拟二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<stdio.h>
#include<stdlib.h>
const int N1=1e8+5;
const int N2=1e2+5;
int pos,len,t;
char tree[N1];
char str[N2];
void create(int pos)//建立二叉树
{
    char c = str[t++];
    if(c == '#')//若是‘#’，说明该节点为空返回上一级节点
        return;
    tree[pos] = c;//若不是‘#’，为本节点赋值
    create(pos*2);//递归创建左子树
    create(pos*2+1);//递归创建右子树
}
void traverse(int root)//中序遍历二叉树
{
    if(tree[root]==0)//如果该节点为0，说明该节点为空，返回上一级
        return;
    traverse(2*root);//先遍历左子树
    printf("%c ",tree[root]);//遍历完左子树后，访问本节点
    traverse(2*root+1);//再遍历右子树
}
int main()
{
    while(scanf("%s",str)!=EOF)
    {
        t=0;
        create(1);
        traverse(1);
        printf("\n");
    }
}
  1. 通过指针创建二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define N 101

struct Node{
    Node *lchild;
    Node *rchild;
    char c;
};

Node *CreateNode()//创建新节点，返回结点指针
{
    Node *ret=(Node*)malloc(sizeof(Node));
    ret->lchild=NULL;
    ret->rchild=NULL;
    return ret;
}

void InOrder(Node *T)//中序遍历
{
    if(T->lchild!=NULL) InOrder(T->lchild);
    printf("%c ", T->c);
    if(T->rchild!=NULL) InOrder(T->rchild);
}

void Del(Node *T)//删除树
{
    if(T->lchild!=NULL)//删除左子树
    {
        Del(T->lchild);
        T->lchild=NULL;
    }
    if(T->rchild!=NULL)//删除右子树
    {
        Del(T->rchild);
        T->rchild=NULL;
    }
    free(T);//删除根节点
}

unsigned pos;//标记字符串处理到哪了
char str[N];//读取的字符串

Node *BuildTree()//根据字符串创立二叉树，并返回根节点指针
{
    if(pos>=strlen(str)) return NULL;//字符串处理完了就歇着吧
    if(str[pos]=='#')//创建空树，即返回空指针
    {
        pos++;//准备处理下一个字符
        return NULL;
    }
    Node *p=CreateNode();//创建一个空节点
    p->c=str[pos++];//先序，先获取根节点的字符信息
    p->lchild=BuildTree();//创建左子树
    p->rchild=BuildTree();//创建右子树
    return p;//完事，返回根节点指针
}

int main()
{
    while(gets(str))
    {
        pos=0;//标记字符串处理到哪了
        Node *T=BuildTree();//根据字符串构建整棵树
        InOrder(T);//中序遍历并输出
        printf("\n");
        Del(T);//贴心的删除树，释放内存空间
    }
}

题目二：给定先序中序求后序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<iostream>
#include<algorithm>
using namespace std;
void Post(string str1,string str2)
{
    if(str1.length()==0)    return;
    int root=str2.find(str1[0]);
    Post(str1.substr(1,root),str2.substr(0,root));
    Post(str1.substr(root+1),str2.substr(root+1));
    cout<<str1[0];
}
int main()
{
    string str1,str2;
    while(cin>>str1>>str2)
    {
        Post(str1,str2);
        cout<<endl;
    }
}

代码二

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <stdio.h>
#include <string.h>
struct Node
{                //树结点结构体
   Node *lchild; //左儿子指针
   Node *rchild; //右儿子指针
   char c;       //结点字符信息
} Tree[50];      //静态内存分配数组
int loc;         //静态数组中已经分配的结点个数
Node *creat()
{  //申请一个结点空间,返回指向其的指针
   Tree[loc].lchild = Tree[loc].rchild = NULL; //初始化左右儿子为空
   return &Tree[loc++];                        //返回指针,且loc累加
}
char str1[30], str2[30]; //保存前序和中序遍历结果字符串
void postOrder(Node *T)
{ //后序遍历
   if (T->lchild != NULL)
   {                        //若左子树不为空
      postOrder(T->lchild); //递归遍历其左子树
   }
   if (T->rchild != NULL)
   {                        //若右子树不为空
      postOrder(T->rchild); //递归遍历其右子树
   }
   printf("%c", T->c); //遍历该结点,输出其字符信息
}
Node *build(int s1, int e1, int s2, int e2)
{  //由字符串的前序遍历和中序遍历还原树, 并返回其根节点, 
   //其中前序遍历结果为由str1[s1] 到str2[e1] ，中序遍历结果为str2[s2] 到str2[e2]
   Node *ret = creat(); //为该树根节点申请空间
   ret->c = str1[s1];   //该结点字符为前序遍历中第一个字符
   int rootIdx;
   for (int i = s2; i <= e2; i++)
   { //查找该根节点字符在中序遍历中的位置
      if (str2[i] == str1[s1])
      {
         rootIdx = i;
         break;
      }
   }
   if (rootIdx != s2)
   {  //若左子树不为空,递归还原其左子树
      ret->lchild = build(s1 + 1, s1 + (rootIdx - s2), s2, rootIdx - 1); 
   }
   if (rootIdx != e2)
   {  //若右子树不为空,递归还原其右子树
      ret->rchild = build(s1 + (rootIdx - s2) + 1, e1, rootIdx + 1, e2); 
   }
   return ret; //返回根节点指针
}
int main()
{
   while (scanf("%s", str1) != EOF)
   {
      scanf("%s", str2); //输入
      loc = 0;    //初始化静态内存空间中已经使用结点个数为0
      int L1 = strlen(str1);
      int L2 = strlen(str2);          //计算两个字符串长度
      Node *T = build(0, L1 - 1, 0, L2 - 1); //还原整棵树,其根结点指针保存在T中
      postOrder(T);                   //后序遍历
      printf("\n");                   //输出换行
   }
   return 0;
}

图论

vector在邻接链表中的应用

首先定义一个结构体

1
2
3
4
typedef Struct Edge{
    int nextNode;//下一个结点编号
    int cost;//该边的权重
}Edge;

为每一个结点建立一个单链表来保存与其相邻的边权值和结点的信息。使用vector来模拟这些单链表。结点数量为N

1
vector<Edge> edge[N];

利用

1
2
3
for(int i=0;i<N;i++)  {
    edge[i].clear();
}

来实现对这些单链表的初始化


要添加信息时使用

1
2
3
4
Edge tmp;//准备一个Edge结构体
tmp.nextNode=3;//下一结点编号为3
tmp.cost=38;
edge[1].push_back(tmp);//将该边加入结点1的单链表中

当需要查询某个结点的所有邻接信息时，对vector进行遍历

1
2
3
4
for(int i=0;i<edge[2].size();i++){
    int nextNode=edge[2][i].nextNode;  //读出邻接结点
    int cost=edge[2][i].cost;  //读出权值
}

当需要删除某个单链表中的某些边信息时，调用vector::erase

例如，删除结点1的单链表中edge[1][i]所对应的边信息时，

1
2
edge[1].erase(edge[1].begin()+i,edge[1].begin())+i+1);
//即vector.erase(vector.begin()+第一个要删除的元素编号，vector.begin()+最后一个要删除元素的编号+1)

并查集

首先，定义一个数组，用双亲表示法来表示各棵树（所有的集合元素个数总和为N）：

1
int Tree[N];

用Tree[i]来表示结点i的双亲结点，若Tree[i]为 -1 则表示该结点不存在双亲结点，即结点i为其所在树的根节点.


为了查找结点x所在树的根节点，定义以下函数

1
2
3
4
5
6
int findRoot(int x)
{
    if(Tree[x]==-1)  return x;//若当前结点为根节点则返回该结点号
    else return findRoot(Tree[x]); //否则递归查找其双钱结点的根节点
}

为了优化路径压缩

1
2
3
4
5
6
7
8
9
int findRoot(int x)
{
    if(Tree[x]==-1)  return x;//若当前结点为根节点则返回该结点号
    else{
        int tmp=findRoot(Tree[x]);
        Tree[x]=tmp; //将当前结点的双亲设置为查找返回的根节点编号
        return tmp;
    }
}

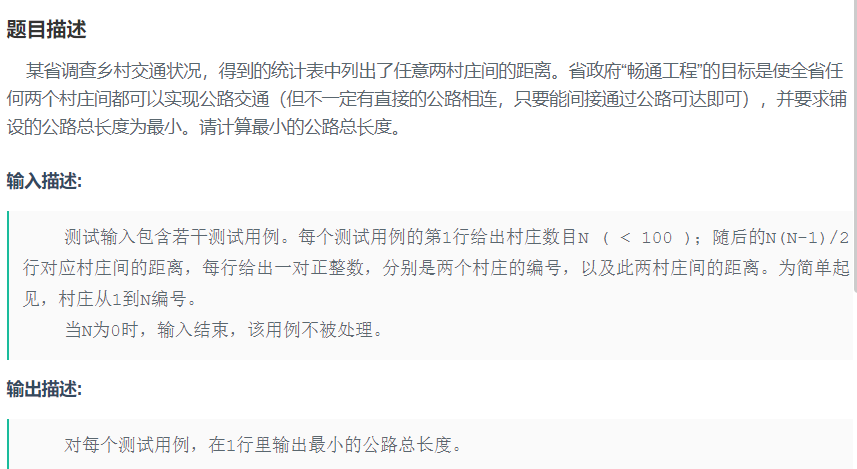
例1 畅通工程 求解图上连通分量个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<iostream>
using namespace std;
int Tree[1010];
void init()
{
    for(int i=0;i<1010;i++)
        Tree[i]=-1;
}
int findRoot(int x)
{
    if(Tree[x]==-1) return x;
    else
    {
        int tmp=findRoot(Tree[x]);
        Tree[x]=tmp;
        return tmp;
    }
}
int main()
{
    int N,M;
    while(cin>>N&&N)
    {
        cin>>M;
        init();
        while(M--)
        {
            int a,b;
            cin>>a>>b;
            
            int roota=findRoot(a);
            int rootb=findRoot(b);
            if(roota!=rootb)
                Tree[roota]=rootb;
        }
        int ans=0;
        for(int i=1;i<=N;i++)
        {
            if(Tree[i]==-1)  ans++;
        }
        cout<<ans-1<<endl; 
    }
    return 0;
}

例2 More is better

题目大意：有10000000个人，其中有n个好朋友，朋友关系具有传递性，找出最大的集合，集合中都是朋友关系或者只有一个人，输出集合中最多少人。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <iostream>
using namespace std;
const int N = 10000001;
int Tree[N] = {0};
int Sum[N] = {0};
void init()
{
    for (int i = 0; i < N; i++)
    {
        Tree[i] = -1;
        Sum[i] = 1;
    }
}

int getRoot(int x)
{
    if (Tree[x] == -1)
        return x;
    else
    {
        int tmp = getRoot(Tree[x]);
        Tree[x] = tmp;
        return tmp;
    }
}
int main()
{
    int n;
    while (cin >> n && n)
    {
        int a, b;
        init();
        while (n--)
        {
            cin >> a >> b;
            a=getRoot(a);
            b=getRoot(b);
            if (a!=b)
            {
                Tree[a] = b;
                Sum[b] += Sum[a];
            }
        }
        int ans = 1;
        for (int i = 0; i < N; i++)
        {
            if (Tree[i] == -1)
            {
                if (Sum[i] > ans)
                {
                    ans = Sum[i];
                }
            }
        }
        cout << ans << endl;
    }
}

可以用来判断连通图

最小生成树

定义：在一个无向连通图中，如果存在一个连通子图包含原图中所有的结点合萼部分边，且这个子图中不存在回路，那么我们称这个子图为原图的一颗生成树。在带权图中，所有的生成树中边权的和最小的那颗（或几颗）被称为最小生成树。

Kruskal算法

原理：

  1. 初始时所有结点属于孤立的集合
  2. 按照边权递增顺序遍历所有的边，若遍历到的边两个顶点仍分属不同的集合（该边即为连通这两个集合的边中权值最小的那条）则确定该边为最小生成树上的一条边，并将这两个顶点分属的集合合并。
  3. 遍历完所有边后，原图上所有结点属于同一个集合则被选取的边和原图中所有结点构成最小生成树；否则原图不连通，最小生成树不存在。。

例题1 还是畅通工程，利用并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include<iostream>
#include<algorithm>
using namespace std;
struct Edge{
    int a;
    int b;
    int cost;
};//定义边数据结构
Edge edge[5000]={0};
int Tree[101]={0};
void init()
{
    for(int i=0;i<101;i++)
        Tree[i]=-1;
}
int findFather(int x)
{
    if(Tree[x]==-1) return x;
    else {
        int tmp=findFather(Tree[x]);
        Tree[x]=tmp;
        return tmp;
    }
}
bool cmp(Edge x,Edge y)
{
    return x.cost<y.cost;
}
int main()
{
    int N;//村庄数目 <100;
    while(cin>>N&&N)
    {
        for(int i=0;i<5000;i++)
            edge[i].a=edge[i].b=edge[i].cost=0;
        int M=N*(N-1)/2;//边的数量;
        for(int i=0;i<M;i++)
           cin>>edge[i].a>>edge[i].b>>edge[i].cost;
        sort(edge,edge+M,cmp);//按边排好序后，选边加入
        init();
        int ans=0;//记录总长度
        for(int i=0;i<M;i++)
        {
            int a=findFather(edge[i].a);
            int b=findFather(edge[i].b);
            if(a!=b)  //不属于一个集合
            {
                Tree[a]=b;
                ans+=edge[i].cost;
            }
        }
        cout<<ans<<endl;
    }
  return 0;
}

最短路径 自己到自己设为0 其他一开始设为-1 不可达

Floyd 弗洛伊德算法

全源最短路 三重循环

1
2
3
4
5
6
7
for(int k=1;k<=n;k++) //k从1到N循环，依次代表允许经过的中间结点编号小于等于k
for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++){
        if(ans[i][k]==-1||ans[k][j]==-1)  continue;
        if(ans[i][j]==-1||ans[i][k]+ans[k][j]<ans[i][j])
            ans[i][j]=ans[i][k]+ans[k][j];
    }

算法特点：最好图的大小不超过200个结点，当两个结点间有多余一条边时，选择长度最小的边权值存入邻接矩阵。

Dijkstra 迪杰斯特拉算法

单源最短路

算法流程：

  1. 初始化，集合K中加入结点1，结点1到结点1最短距离为0，到其他结点为无穷（或不确定）
  2. 遍历与集合K中结点直接相邻的边（U，V，C），其中U属于集合K，V不属于集合K，计算由结点1出发按照已经得到的最短路径到达U，再由U经过该边到达V时的路径长度。比较所有与集合K中结点直接相邻的非集合K结点该路径长度，其中路径长度最小的结点被确定为下一个最短路径确定的结点，其最短路径长度即为这个路径长度，最后将该结点加入集合K
  3. 若集合K中已经包含所有的点，算法结束；否则重复步骤2

例题
采用vector模拟链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<iostream>
#include<vector>
using namespace std;
struct E{
    int next;  //代表直接相邻的结点
    int c;     //代表该边的权值
};
vector<E> edge[101];//邻接链表
bool mark[101];//标记是否得到最短路径
int Dis[101];//标记开始点距离各个结点距离
int main()
{
    int n,m;
    while(cin>>n>>m&&n&&m)
    {
        for(int i=1;i<=n;i++)  
            edge[i].clear(); //初始化邻接链表
        while(m--)
        {
            int a,b,c;
            cin>>a>>b>>c;
            E tmp;
            tmp.c=c;
            tmp.next=b;
            edge[a].push_back(tmp);
            tmp.next=a;
            edge[b].push_back(tmp);
            //将邻接信息加入邻接链表，无向图 两遍
        }
        //初始化mark和dis数组
        for(int i=1;i<=n;i++)
        {
            Dis[i]=-1;//代表不可达
            mark[i]=false;//所有结点不属于集合K
        }
        Dis[1]=0; //得到最近的结点为自己 结点1，长度为0
        mark[1]=true;//将结点1加入集合K
        int newP=1;//集合中新加入的点为结点1
        for(int i=1;i<n;i++)//循环n-1次
        {
            for(int j=0;j<edge[newP].size();j++){
                int t=edge[newP][j].next;
                int c=edge[newP][j].c;
                //看是否可通过newP这个点 缩短相关结点的最短距离
                if(mark[t]==true) continue;
                if(Dis[t]==-1||Dis[t]>Dis[newP]+c)
                {
                    Dis[t]=Dis[newP]+c;
                }
            }
            //找下一个最小点   之前的标记为true
            int min=123123123;//最小值初始化为一个大整数，为找最小值作准备
            for(int j=1;j<=n;j++){
                if(mark[j]==true) continue;
                if(Dis[j]==-1) continue;
                if(Dis[j]<min){
                    min=Dis[j]; //更新其为最小值
                    newP=j; //以此为中介 更新
                }
            }
            mark[newP]=true;
        }
        cout<<Dis[n]<<endl;
    }
    return 0;
}

采用矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
需要一个辅助数组dis来存储起点到其他所有点的距离
将dis数组中的值称为最短路程的"估计值"
核心思想:通过边来松弛起点到其他各个点的距离
代码;
//初始化dis数组
 for(int i=1;i<=n;i++)
  dis[i]=a[1][i](假设起点为1)
//标记数组初始化visted
 for(int i=1;i<=n;i++)
   visted[i]=0;
 visted[1]=1;
//接下来重复过程
在dis数组中找当前离起点最近的点
然后访问这个点的所有边看是否能通过dis数组更新起点到那些边的距离
能的话就更新
代码:(部分是伪代码)
 int min=Inf;
 for(int i=1;i<=dis.size();i++)
  {
    if(dis[i]<min)
     {
        min=dis[i];
        mark=i  ;//mark用来记录这一点
     } 
}
然后更新：
 for(int v=1；v<=n;v++)
   {
      if(a[mark][v]<inf)
        {
             if(dis[v]>dis[mark]+a[mark][v])
                dis[v]=dis[mark]+a[mark][v];
        }
   }

这个过程持续n-1所以最外层还要加上循环
 for(int k=1;k<=n-1;k++)
{
 ….
}

时间复杂度O(n^2)


拓扑排序

使用标准模版：std：：queue

1
queue<int> Q;

Q.push(x);将元素x放入队尾

x=Q.front();//读取队头元素，将其值赋值给x

Q.pop();//弹出队头元素

Q.empty();//判断队列是否为空，若返回值为true代表队列为空

为了保存在拓扑排序中不断出现的和之前已经出现的入度为 0 的结点，我们 使用一个队列。每当出现一个入度为 0 的结点，我们将其放入队列；若需要找到 一个入度为 0 的结点，就从队头取出。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// 在一个 qq 群里有着许多师徒关系，如 A 是 B 的师父，同时 B
// 是A的徒弟，一个师父可能有许多徒弟，一个徒弟也可能会有许多不同的师父。 
// 输入给出该群里所有的师徒关系，问是否存在这样一种非法的情况：
// 以三个人为 例，即A是B的师父，B是C 的师父，C又反过来是A的师父。
// 若我们将该群 里的所有人都抽象成图上的结点，将所有的师徒关系都抽象成有向边（由师父指 向徒弟），
// 该实际问题就转化 图是否为有向无环图。为一个数学问题——该图上是否存在一个环，
// 即判断是否属于有向无环图时。若一个图，存在符合拓扑次序的结点序列，则该图为有向无环图
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
vector<int> edge[501];//邻接链表，此边无权值，只需保存编号
queue<int> Q;//保存入度为0的结点的队列
int main()
{
    int inDegree[501];//统计每个结点的入度
    int n,m;
    while(cin>>n>>m&&n&&m)
    {
        for(int i=0;i<n;i++)//初始化所有结点，编号0~n-1
        {
            inDegree[i]=0; //初始化入度信息，所有结点入度均为0
            edge[i].clear();//清空邻接链表
        }
        while (m--)
        {
            int a,b;
            cin>>a>>b;//读入一条由a指向b的有向边
            inDegree[b]++;
            edge[a].push_back(b);//将b加入a的邻接链表
        }
        while(Q.empty()==false) Q.pop();//清空队列
        for(int i=0;i<n;i++){
            if(inDegree[i]==0)
            Q.push(i);//若结点入度为0，则将其放入队列
        }
        int cnt=0;//累加已经确定拓扑序列的结点个数
        while(Q.empty()==false){
            int nowP=Q.front();//取出队头结点编号
            Q.pop();//弹出队头元素
            cnt++;
            for(int i=0;i<edge[nowP].size();i++){
                //将该结点以及以其为弧尾的所有边去除
                inDegree[edge[nowP][i]]--;
                //去除某条边后，该边所指后继结点入度减一
                if(inDegree[edge[nowP][i]]==0){
                //若该结点入度变为0
                Q.push(edge[nowP][i]);//将其放到队列中
                }

            }
        }
        //若所有结点都能被确定拓扑序列，则原图为有向无环图
        //否则，原图为非有向无环图
        if(cnt==n) cout<<"YES";
        else cout<<"NO";
        cout<<endl;
    }
    return 0;
}
算法
#总结 #算法
数据结构相关算法
https://shanhainanhua.github.io/2021/03/01/数据结构相关算法/
作者
wantong
发布于
2021年3月1日
许可协议