编程实现KNN和朴素贝叶斯算法分类
大数据上机作业,编程实现K近邻和朴素贝叶斯算法
1、 编程实现KNN算法对下表中两个未知类型的样本进行分类(冰川水或者湖泊水),其中K=3,即选择最近的3个邻居。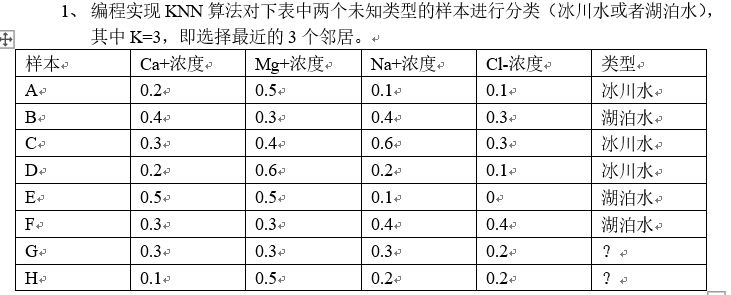
1 | |
计算两者之间距离为0.31622776601683794
计算两者之间距离为0.17320508075688776
计算两者之间距离为0.33166247903553997
计算两者之间距离为0.34641016151377546
计算两者之间距离为0.4
计算两者之间距离为0.22360679774997902
湖泊水
计算两者之间距离为0.17320508075688776
计算两者之间距离为0.42426406871192857
计算两者之间距离为0.4690415759823429
计算两者之间距离为0.17320508075688773
计算两者之间距离为0.45825756949558405
计算两者之间距离为0.4
冰川水
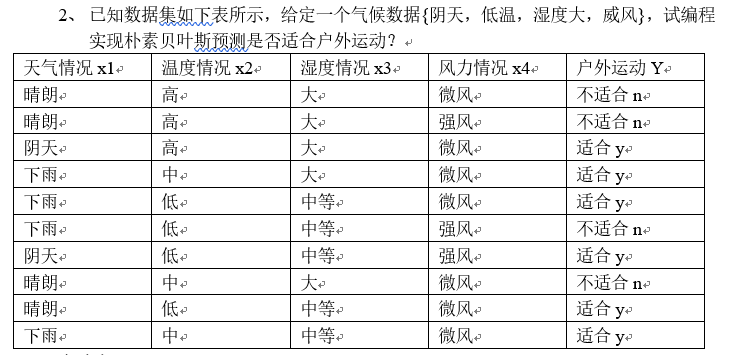
实现朴素贝叶斯算法预测是否适合户外活动
1 | |
标签适合的概率为0.6
传入的要检查的x值为下雨
3
传入的要检查的x值为低
3
传入的要检查的x值为大
2
传入的要检查的x值为微风
5
0.041666666666666664
标签不适合的概率为0.4
传入的要检查的x值为下雨
1
传入的要检查的x值为低
1
传入的要检查的x值为大
3
传入的要检查的x值为微风
2
0.009375000000000001
适合概率为0.041666666666666664
不适合概率为0.009375000000000001
最终答案为适合
编程实现KNN和朴素贝叶斯算法分类
https://shanhainanhua.github.io/2019/10/19/编程实现KNN和朴素贝叶斯算法分类/