监督学习之k近邻

监督学习之k近邻

所需要的所有包

1
2
3
4
5
6
7
8
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import mglearn
%matplotlib inline
# 由于 %matplotlib inline 的存在，当输入plt.plot(x,y_1)后，不必再输入 plt.show()
#图像将自动显示出来

1.k近邻分类

1
2
3
4
import mglearn
%matplotlib inline
mglearn.plots.plot_knn_classification(n_neighbors=1)

png

除了仅考虑最近邻，我还可以考虑任意个（k 个）邻居。这也是 k 近邻算法名字的来历。在考虑多于一个邻居的情况时，我们用“投票法”（voting）来指定标签。也就是说，对于每个测试点，我们数一数多少个邻居属于类别 0，多少个邻居属于类别 1。然后将出现次数更多的类别（也就是 k 个近邻中占多数的类别）作为预测结果。下面的例子（图 2-5）用到了 3 个近邻：

1
mglearn.plots.plot_knn_classification(n_neighbors=3)

png

通过scikit-learn来应用k近邻算法

  • 导入类并将其实例化。这时可以设定参数，如邻居的个数
  • 利用训练集对这个分类器进行拟合
  • 调用 predict 方法来对测试数据进行预测
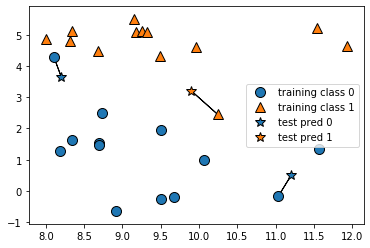
1
2
3
4
5
6
7
8
9
from sklearn.model_selection import train_test_split
X,y=mglearn.datasets.make_forge()
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)

from sklearn.neighbors import KNeighborsClassifier
clf=KNeighborsClassifier(n_neighbors=3)
clf.fit(X_train,y_train)
print("Test set predictions: {}".format(clf.predict(X_test)))
print("Test set accuracy: {:.2f}".format(clf.score(X_test,y_test)))
Test set predictions: [1 0 1 0 1 0 0]
Test set accuracy: 0.86

2.分析KNeighborsClassifier

对于二维数据集，我们还可以在 xy 平面上画出所有可能的测试点的预测结果。我们根据平面中每个点所属的类别对平面进行着色。这样可以查看决策边界（decision boundary），即算法对类别 0 和类别 1 的分界线。

zip() 函数用于将可迭代的对象作为参数，将对象中对应的元素打包成一个个元组，然后返回由这些元组组成的列表。

zip 方法在 Python 2 和 Python 3 中的不同：在 Python 3.x 中为了减少内存，zip() 返回的是一个对象。如需展示列表，需手动 list() 转换。

subplots参数与subplots相似。

两者都可以规划figure划分为n个子图，但每条subplot命令只会创建一个子图，而一条subplots就可以将所有子图创建好。

subplots用法示例如下：

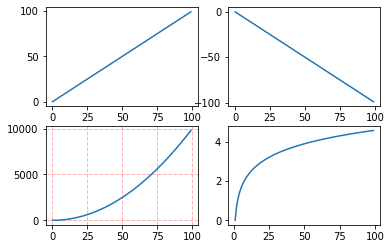
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
import matplotlib.pyplot as plt
 
x = np.arange(0, 100)
#划分子图
fig,axes=plt.subplots(2,2)
ax1=axes[0,0]
ax2=axes[0,1]
ax3=axes[1,0]
ax4=axes[1,1]
 
#作图1
ax1.plot(x, x)
#作图2
ax2.plot(x, -x)
#作图3
ax3.plot(x, x ** 2)
ax3.grid(color='r', linestyle='--', linewidth=1,alpha=0.3)
#作图4
ax4.plot(x, np.log(x))
plt.show()

png

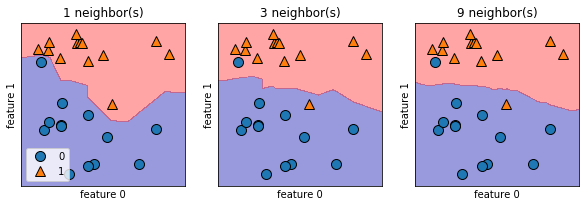
1
2
3
4
5
6
7
8
9
fig,axes=plt.subplots(1,3,figsize=(10,3))
for n_neighbors,ax in zip([1,3,9],axes):
    clf=KNeighborsClassifier(n_neighbors=n_neighbors).fit(X,y)
    mglearn.plots.plot_2d_separator(clf,X,fill=True,eps=0.5,ax=ax,alpha=.4)
    mglearn.discrete_scatter(X[:,0],X[:,1],y,ax=ax)
    ax.set_title("{} neighbor(s)".format(n_neighbors))
    ax.set_xlabel("feature 0")
    ax.set_ylabel("feature 1")
axes[0].legend(loc=3)
<matplotlib.legend.Legend at 0x242302ba9b0>

png

用单一邻居绘制的决策边界紧跟着训练数据。随着邻居个数越来越多，决策边界也越来越平滑。更平滑的边界对应更简单的模型。换句话说，使用更少的邻居对应更高的模型复杂度，而使用更多的邻居对应更低的模型复杂度。假如考虑极端情况，即邻居个数等于训练集中所有数据点的个数，那么每个测试点的邻居都完全相同（即所有训练点），所有预测结果也完全相同（即训练集中出现次数最多的类别）。

在现实世界的乳腺癌数据集上进行研究，证实模型复杂度和泛化能力的关系

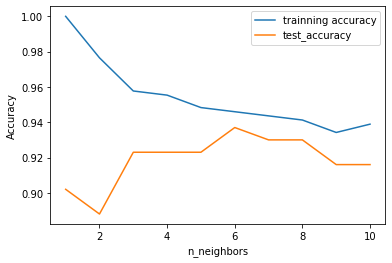
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn import neighbors
cancer=load_breast_cancer()  #加载癌症数据集
X_train,X_test,y_train,y_test=train_test_split(cancer.data,cancer.target,
                                                stratify=cancer.target,random_state=66)

training_accuracy=[]
test_accuracy=[]

#neighbors取值从1到10
neighbors_settings=range(1,11)

for n_neighbors in neighbors_settings:
    clf=KNeighborsClassifier(n_neighbors=n_neighbors)
    clf.fit(X_train,y_train)
    training_accuracy.append(clf.score(X_train,y_train))
    test_accuracy.append(clf.score(X_test,y_test))
    
plt.plot(neighbors_settings,training_accuracy,label="trainning accuracy")
plt.plot(neighbors_settings,test_accuracy,label="test_accuracy")
plt.ylabel("Accuracy")
plt.xlabel("n_neighbors")
plt.legend()

<matplotlib.legend.Legend at 0x24230a4b5c0>

png

仅考虑单一近邻时，训练集上的预测结果十分完美。但随着邻居个数的增多，模型变得更简单，训练集精度也随之下降。单一邻居时的测试集精度比使用更多邻居时要低，这表示单一近邻的模型过于复杂。与之相反，当考虑 10 个邻居时，模型又过于简单，性能甚至变得更差。最佳性能在中间的某处，邻居个数大约为 6。不过最好记住这张图的坐标轴刻度。最差的性能约为 88% 的精度，这个结果仍然可以接受。

3.K近邻回归

k近邻算法还可以用于回归(把邻居的平均值赋给目标)。

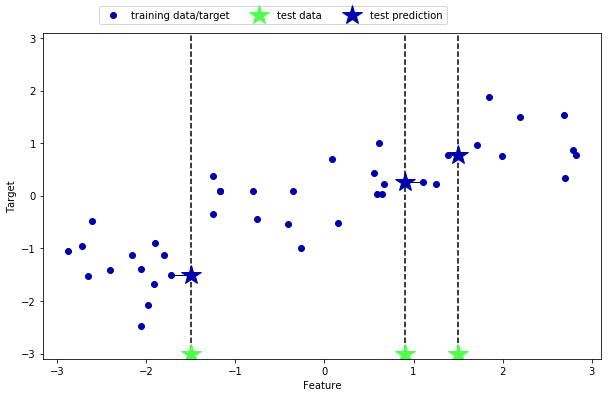
1
mglearn.plots.plot_knn_regression(n_neighbors=1)

png

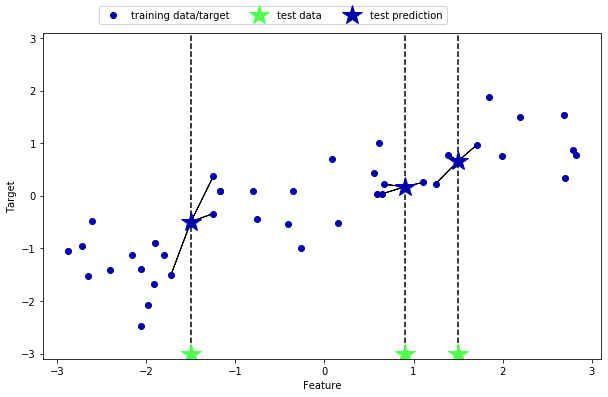
用多个近邻进行回归,预测结果为这些邻居的平均值

1
mglearn.plots.plot_knn_regression(n_neighbors=3)

png

用于回归的k近邻算法在sklearn的KNeighborsRegressor类中实现

1
2
3
4
5
6
7
8
9
10
from sklearn.neighbors import KNeighborsRegressor
X,y=mglearn.datasets.make_wave(n_samples=40)
# 划分训练数据集
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0)
# 实例化模型，邻居设定为3
reg=KNeighborsRegressor(n_neighbors=3)
# 拟合模型
reg.fit(X_train,y_train)


KNeighborsRegressor(algorithm='auto', leaf_size=30, metric='minkowski',
                    metric_params=None, n_jobs=None, n_neighbors=3, p=2,
                    weights='uniform')

1
2
3
4
5

print("Test set predictions:\n{}".format(reg.predict(X_test)))
print("Test set R^2:{:.2f}".format(reg.score(X_test,y_test)))


Test set predictions:
[-0.05396539  0.35686046  1.13671923 -1.89415682 -1.13881398 -1.63113382
  0.35686046  0.91241374 -0.44680446 -1.13881398]
Test set R^2:0.83

可以用score方法来评估模型，对于回归问题，这一方法返回的是$R^2$分数，也叫做决定系数，是回归模型预测的优度度量，位于0到1之间，1完美预测，0对于常数模型，即总是预测训练集响应(y_train)的平均值

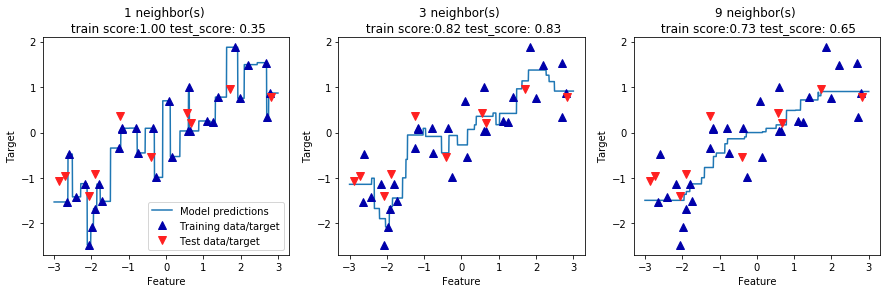
4.分析KNeigborsRegressor

对于我们的一维数据集，可以查看所有特征取值对应的预测结果（图 2-10）。为了便于绘
图，我们创建一个由许多点组成的测试数据集

np reshape array linespace 用法：
numpy.arange(n).reshape(a, b); 依次生成n个自然数，并且以a行b列的数组形式显示

1
2
3
import numpy as np
print(np.array([1,1,1]).reshape(3,1))

[[1]
 [1]
 [1]]

1
print(np.linspace(1,100,2).reshape(2,-1))
[[  1.]
 [100.]]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
fig,axes=plt.subplots(1,3,figsize=(15,4))
#创建1000个数据点，在-3和3之间均匀分布
line=np.linspace(-3,3,1000).reshape(-1,1)
for n_neighbors,ax in zip([1,3,9],axes):
    reg=KNeighborsRegressor(n_neighbors=n_neighbors)
    reg.fit(X_train,y_train)
    ax.plot(line,reg.predict(line))
    ax.plot(X_train,y_train,'^',c=mglearn.cm2(0),markersize=8)
    ax.plot(X_test,y_test,'v',c=mglearn.cm2(1),markersize=8)
    ax.set_title(
    "{} neighbor(s) \n train score:{:.2f} test_score: {:.2f}".format(
    n_neighbors,reg.score(X_train,y_train),reg.score(X_test,y_test)))
    ax.set_xlabel("Feature")
    ax.set_ylabel("Target")
axes[0].legend(["Model predictions","Training data/target",
               "Test data/target"],loc="best")

<matplotlib.legend.Legend at 0x2422e47e5c0>

png

从图中可以看出，仅使用单一邻居，训练集中的每个点都对预测结果有显著影响，预测结果的图像经过所有数据点。这导致预测结果非常不稳定。考虑更多的邻居之后，预测结果变得更加平滑，但对训练数据的拟合也不好。

5.优点，缺点和参数

一般来说， KNeighbors 分类器有 2 个重要参数：邻居个数与数据点之间距离的度量方法。在实践中，使用较小的邻居个数（比如 3 个或 5 个）往往可以得到比较好的结果，但你应该调节这个参数。选择合适的距离度量方法超出了本书的范围。默认使用欧式距离，它在许多情况下的效果都很好。

k-NN 的优点之一就是模型很容易理解，通常不需要过多调节就可以得到不错的性能。在考虑使用更高级的技术之前，尝试此算法是一种很好的基准方法。构建最近邻模型的速度通常很快，但如果训练集很大（特征数很多或者样本数很大），预测速度可能会比较慢。使用 k-NN 算法时，对数据进行预处理是很重要的（见第 3 章）。这一算法对于有很多特征（几百或更多）的数据集往往效果不好，对于大多数特征的大多数取值都为 0 的数据集（所谓的稀疏数据集）来说，这一算法的效果尤其不好。

虽然 k 近邻算法很容易理解，但由于预测速度慢且不能处理具有很多特征的数据集，所以在实践中往往不会用到

机器学习
监督学习之k近邻
https://shanhainanhua.github.io/2019/10/05/监督学习之k近邻/
作者
wantong
发布于
2019年10月5日
许可协议